题目内容
已知数列{an}中各项为:12、1122、111222、
(1)证明这个数列中的每一项都是两个相邻整数的积.
(2)求这个数列前n项之和Sn.
| ||
| 个n |
| ||
| n个 |
(1)证明这个数列中的每一项都是两个相邻整数的积.
(2)求这个数列前n项之和Sn.
(1)an=
(10n-1)•10n+
(10n-1)(2分)
=
(10n-1)(10n+2)=(
)(
+1)(4分)
记:A=
,则A=
为整数
∴an=A(A+1),得证(6分)
(2)∵an=
102n+
10n-
(8分)
Sn=
(102+104+…+102n)+
(10+102+…+10n)-
n
=
(102n+2)+11•10n+1-198n-210(12分)
| 1 |
| 9 |
| 2 |
| 9 |
=
| 1 |
| 9 |
| 10n-1 |
| 3 |
| 10n-1 |
| 3 |
记:A=
| 10n-1 |
| 3 |
| ||
| n个 |
∴an=A(A+1),得证(6分)
(2)∵an=
| 1 |
| 9 |
| 1 |
| 9 |
| 2 |
| 9 |
Sn=
| 1 |
| 9 |
| 1 |
| 9 |
| 2 |
| 9 |
=
| 1 |
| 891 |

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
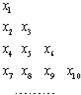 若一个数列各项取倒数后按原来的顺序构成等差数列,则称这个数列为调和数列.已知数列{an}是调和数列,对于各项都是正数的数列{xn},满足
若一个数列各项取倒数后按原来的顺序构成等差数列,则称这个数列为调和数列.已知数列{an}是调和数列,对于各项都是正数的数列{xn},满足