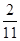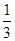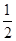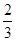题目内容
以下四个命题中：
①为了了解800名学生对学校某项教改试验的意见，打算从中抽取一个容量为
的
样本，考虑用系统抽样，则分段的间隔
为40；
②线性回归直线方程
恒过样本中心
，且至少过一个样本点；
③在某项测量中，测量结果
~
，若在
内取值的概率为
，则在
内取值的概率为
.其中真命题的个数为（ ）
A． | B． | C． | D． |
B
解析试题分析：：①由题意知本题是一个系统抽样，总体中个体数是800，样本容量是40，根据系统抽样的步骤，得到分段的间隔
，故①是假命题；
②线性回归直线方程
恒过样本中心
，但不一定过样本点，故②是假命题；
③由于服从正态分布
，则正态分布图象的对称轴为
，
故在
内取值的概率为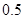
，
又由在
内取值的概率为，则在
内取值的概率为
故在
内取值的概率为，故③是真命题；
考点：线性回归方程；正态分布曲线的特点及曲线所表示的意义．
已知样本7,10,14,8,7,12,11,10,8,10,13,10,8,11,8,9,12,9,13,20,那么这组数据落在8.5～11.5的频率为（ ）
| A．0.5 | B．0.4 | C．0.3 | D．0.2 |
一个容量为20的样本，数据的分组及各组的频数如下：
（10，20
，2；（20，30，3；（30，40，4；（40，50，5；（50，60，4；（60，70，2.
则样本在区间（10，50上的频率为（ ）
| A．0.5 | B．0.7 | C．0.25 | D．0.05 |
在独立性检验中，统计量
有两个临界值：3.841和6.635；当＞3.841时，有95%的把握说明两个事件有关，当＞6.635时，有99%的把握说明两个事件有关，当
3.841时，认为两个事件无关.在一项打鼾与患心脏病的调查中，共调查了2000人，经计算的="20." 87，根据这一数据分析，认为打鼾与患心脏病之间
| A．有95%的把握认为两者有关 |
| B．约有95%的打鼾者患心脏病 |
| C．有99%的把握认为两者有关 |
| D．约有99%的打鼾者患心脏病 |
为了了解
名学生的学习情况，采用系统抽样的方法，从中抽取容量为
的样本，则分段的间隔为（ ）
A． | B． | C． | D． |
在独立性检验中，统计量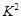
有两个临界值：3.841和6.635；当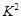＞3.841时，有95%的把握说明两个事件有关，当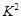＞6.635时，有99%的把握说明两个事件有关，当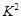
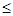3.841时，认为两个事件无关.在一项打鼾与患心脏病的调查中，共调查了2000人，经计算的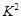=20.87，根据这一数据分析，认为打鼾与患心脏病之间 ( )
| A．有95%的把握认为两者有关 | B．约有95%的打鼾者患心脏病 |
| C．有99%的把握认为两者有关 | D．约有99%的打鼾者患心脏病 |
某单位有27名老年人， 54名中年人，81名青年人. 为了调查他们的身体情况，用分层抽样的方法从他们中抽取了n个人进行体检，其中有6名老年人，那么n=（ ）
| A．35 | B．36 | C．37 | D．162 |
