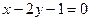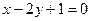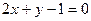题目内容
设函数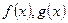 的定义域分别为F,G,且
的定义域分别为F,G,且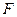 是G的真子集。若对任意的
是G的真子集。若对任意的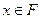 ,都有
,都有 ,则称
,则称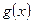 为
为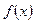 在G上的一个“延拓函数”。已知函数
在G上的一个“延拓函数”。已知函数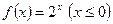 ,若
,若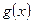 为
为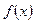 在R上的一个“延拓函数”,且
在R上的一个“延拓函数”,且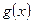 是偶函数,则函数
是偶函数,则函数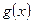 的解析式是( )
的解析式是( )
A.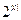 | B.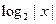 | C.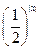 | D. |
C
解析

练习册系列答案
 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案
相关题目
函数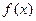 是定义域为R的奇函数,当
是定义域为R的奇函数,当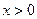 时,
时,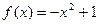 ,则当
,则当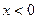 时,
时,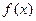 的表达式为 ( )
的表达式为 ( )
A.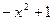 | B.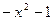 | C.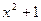 | D.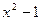 |
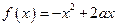 与
与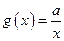 在
在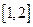 上都为减函数,则
上都为减函数,则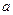 范围是( )
范围是( )
A. | B.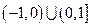  | C.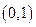 | D.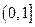 |
下列各组函数中,表示同一函数的是( )
⑴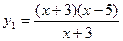 ,
,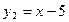 ;
;
⑵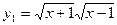 ,
,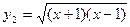 ;
;
⑶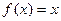 ,
,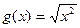 ;
;
⑷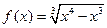 ,
,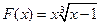 ;
;
⑸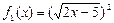 ,
,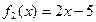 。
。
| A.⑴、⑵ | B.⑵、⑶ | C.⑷ | D.⑶、⑸ |
已知函数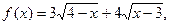 则函数
则函数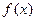 的最大值为 ( )
的最大值为 ( )
| A.3 | B.4 | C.5 | D.不存在 |
函数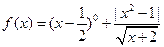 的定义域为( )
的定义域为( )
A.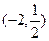 | B.(-2,+∞) | C.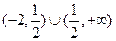 | D.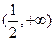 |
函数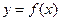 的图象与
的图象与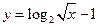 的图象关于直线
的图象关于直线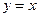 对称,则
对称,则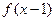 =( )
=( )
A.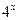 | B.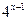 | C.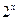 | D.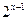 |
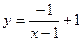 的图象是下列图象中的 ( )
的图象是下列图象中的 ( )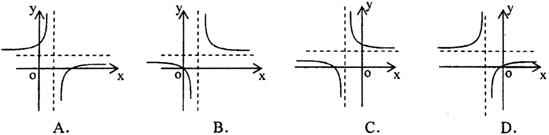
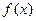 存在反函数
存在反函数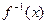 ,且函数
,且函数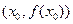 处的切线方程为
处的切线方程为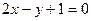 ,则函数
,则函数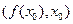 处的切线方程为 ( )
处的切线方程为 ( )