题目内容
 如图,在四面体ABOC中,OC⊥OA,OC⊥OB,∠AOB=120°,且OA=OB=OC=1.
如图,在四面体ABOC中,OC⊥OA,OC⊥OB,∠AOB=120°,且OA=OB=OC=1.①设P为AC的中点.证明:在AB上存在一点Q,使PQ⊥OA,并计算
| AB | AQ |
②求四面体PAOB的体积.
分析:①如图所示,取OA的中点M,过点M作MQ⊥AB,垂足为Q,连接PQ,则PM∥OC,于是可得PQ⊥OA.利用三角形的中位线定理和线面垂直的判定与性质定理即可证明;
②分别计算PM=
OC,S△AMQ=
AM•AQ•sin30°,利用VP-AMQ=
×PM×S△AMQ即可得出.
②分别计算PM=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
解答:解:①如图所示, 取OA的中点M,过点M作MQ⊥AB,垂足为Q,连接PQ,则PM∥OC,于是可得PQ⊥OA.
取OA的中点M,过点M作MQ⊥AB,垂足为Q,连接PQ,则PM∥OC,于是可得PQ⊥OA.
证明如下:∵OC⊥OA,OC⊥OB,OA∩OB=O,∴OC⊥平面OAB.
又PM∥OC,∴AM⊥平面OAB,∴PM⊥OA.
∵MQ⊥OA,MP∩MQ=M,∴OA⊥平面MPQ,∴OA⊥PQ.
下面计算
的值在△OAB中,∠AOB=120°,OA=OB=1,∴∠A=30°.AM=
.
由余弦定理可得AB2=2OA2-2OA2•cos120°=3,∴AB=
.
在Rt△AMQ中,AQ=
=
.
∴
=
.
②∵PM=
OC=
.S△AMQ=
AM•AQ•sin30°=
.
∴VP-AMQ=
×PM×S△AMQ=
×
×
=
.
 取OA的中点M,过点M作MQ⊥AB,垂足为Q,连接PQ,则PM∥OC,于是可得PQ⊥OA.
取OA的中点M,过点M作MQ⊥AB,垂足为Q,连接PQ,则PM∥OC,于是可得PQ⊥OA.证明如下:∵OC⊥OA,OC⊥OB,OA∩OB=O,∴OC⊥平面OAB.
又PM∥OC,∴AM⊥平面OAB,∴PM⊥OA.
∵MQ⊥OA,MP∩MQ=M,∴OA⊥平面MPQ,∴OA⊥PQ.
下面计算
| AB |
| AQ |
| 1 |
| 2 |
由余弦定理可得AB2=2OA2-2OA2•cos120°=3,∴AB=
| 3 |
在Rt△AMQ中,AQ=
| AM |
| cos30° |
| ||
| 3 |
∴
| AQ |
| AB |
| 1 |
| 3 |
②∵PM=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 24 |
∴VP-AMQ=
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
| ||
| 24 |
| ||
| 144 |
点评:本题考查了线面垂直的判定与性质定理、三角形的中位线定理、直角三角形的边角关系、余弦定理、三棱锥的体积计算公式等基础知识与基本技能方法,属于难题.

练习册系列答案
 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案
相关题目
 如图,在四面体ABOC中,OC⊥OA,OC⊥OB,∠AOB=120°,且OA=OB=OC=1
如图,在四面体ABOC中,OC⊥OA,OC⊥OB,∠AOB=120°,且OA=OB=OC=1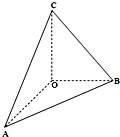 如图,在四面体ABOC中,OC⊥OA,OC⊥OB,∠AOB=120°,且OA=OB=OC=1
如图,在四面体ABOC中,OC⊥OA,OC⊥OB,∠AOB=120°,且OA=OB=OC=1 如图,在四面体ABOC中,OC⊥OA,OC⊥OB,∠AOB=120°,且OA=OB=OC=1.
如图,在四面体ABOC中,OC⊥OA,OC⊥OB,∠AOB=120°,且OA=OB=OC=1. 的值;
的值;