题目内容
已知等比数列{an}的前n项和为 ,数列{bn}(bn>0)的首项为c,且前n项和T(n)满足
,数列{bn}(bn>0)的首项为c,且前n项和T(n)满足 (n≥2).
(n≥2).
(1)设 ,求证数列{dn}为等差数列,并求其通项公式;
,求证数列{dn}为等差数列,并求其通项公式;
(2)求数列{an}和{bn}的通项公式;
(3)若数列{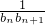 }前n项和为P(n),问P(n)>
}前n项和为P(n),问P(n)> 的最小正整数n是多少?.
的最小正整数n是多少?.
解:(1)由 得
得
数列{an}是等比数列得:
所以c=1.(2分)
因为bn>0所以T(n)>0 ,n≥2
,n≥2
即d(n)-d(n-1)=1,d(1)=1所以数列{dn}为等差数列.d(n)=n,T(n)=n2(6分)
(2)∵b1=1,bn=n2-(n-1)2=2n-1,当n=1时,2n-1=b1,∴bn=2n-1
∵{an}是等比数列,得 ,c=1,
,c=1,
∴ (10分)
(10分)
(3)
=
= (12分)
(12分)
所以

所以适合条件的最小正整数n的值为112.(15分)
分析:(1)由 得
得 ,再由{an}是等比数列得
,再由{an}是等比数列得 ,由此能证明数列{dn}为等差数列,并能求出其通项公式.
,由此能证明数列{dn}为等差数列,并能求出其通项公式.
(2))由b1=1,bn=n2-(n-1)2=2n-1和{an}是等比数列, ,c=1,能导出bn=2n-1,
,c=1,能导出bn=2n-1, .
.
(3) =
= =
= ,由此能求出适合条件的最小正整数n的值为112.
,由此能求出适合条件的最小正整数n的值为112.
点评:本题考查数列的性质和应用,解题时要认真审题,仔细解答.
 得
得
数列{an}是等比数列得:

所以c=1.(2分)
因为bn>0所以T(n)>0
 ,n≥2
,n≥2即d(n)-d(n-1)=1,d(1)=1所以数列{dn}为等差数列.d(n)=n,T(n)=n2(6分)
(2)∵b1=1,bn=n2-(n-1)2=2n-1,当n=1时,2n-1=b1,∴bn=2n-1
∵{an}是等比数列,得
 ,c=1,
,c=1,∴
 (10分)
(10分)(3)

=

=
 (12分)
(12分)所以


所以适合条件的最小正整数n的值为112.(15分)
分析:(1)由
 得
得 ,再由{an}是等比数列得
,再由{an}是等比数列得 ,由此能证明数列{dn}为等差数列,并能求出其通项公式.
,由此能证明数列{dn}为等差数列,并能求出其通项公式.(2))由b1=1,bn=n2-(n-1)2=2n-1和{an}是等比数列,
 ,c=1,能导出bn=2n-1,
,c=1,能导出bn=2n-1, .
.(3)
 =
= =
= ,由此能求出适合条件的最小正整数n的值为112.
,由此能求出适合条件的最小正整数n的值为112.点评:本题考查数列的性质和应用,解题时要认真审题,仔细解答.

练习册系列答案
 核心素养学练评系列答案
核心素养学练评系列答案 单元期中期末卷系列答案
单元期中期末卷系列答案
相关题目