Question

【题目】已知函数f（x）=ax﹣1﹣lnx（a∈R）．
（1）当a=1时，求曲线在点（1，0）处的切线方程；
（2）求函数f（x）在区间 上的最小值．

Answer 1

【答案】
（1）解：函数f（x）的定义域为（0，+∞），

当a=1时，f′（x）=1﹣ ，则f'（1）=0，故曲线在点（1，0）处的切线为y=0

（2）解：f′（x）= （x＞0），则：

①当a≤0时，f'（x）＜0，

此时f（x）在[ ，2]上单减，故f（x）min=f（2）=2a﹣1﹣ln2

②当a＞0时，

（Ⅰ）0＜ ≤ ，即a≥2，f（x）在上单增，故f（x）min=f（ ）= ﹣1+ln2；

（Ⅱ） ＜ ＜2，即 ＜a＜2，f（x）在[ ， ）单减，在[ ，2]单增，故f（x）min=f（ ）=lna．

（Ⅲ） ≥2，即0＜a≤ ，f（x）在[ ，2]上单减，故f（x）min=f（2）=2a﹣1﹣ln2，

综上f（x）min=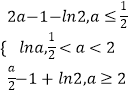

【解析】（1）利用导数与曲线斜率的公式即可求得结论；（2）分类讨论，利用导数即可求得函数的最小值．
【考点精析】本题主要考查了函数的最大(小)值与导数的相关知识点，需要掌握求函数在上的最大值与最小值的步骤：（1）求函数在内的极值；（2）将函数的各极值与端点处的函数值，比较，其中最大的是一个最大值，最小的是最小值才能正确解答此题．