题目内容
已知椭圆![]() 的两焦点与短轴的一个端点的连线构成等腰直角三角形,直线
的两焦点与短轴的一个端点的连线构成等腰直角三角形,直线![]() 是抛物线
是抛物线![]() 的一条切线.
的一条切线.
(Ⅰ)求椭圆的方程;
(Ⅱ)过点![]() 的动直线L交椭圆C于A、B两点.问:是否存在一个定点T,使得以AB为直径的圆恒过点T ? 若存在,求点T坐标;若不存在,说明理由.
的动直线L交椭圆C于A、B两点.问:是否存在一个定点T,使得以AB为直径的圆恒过点T ? 若存在,求点T坐标;若不存在,说明理由.
(Ⅰ)![]()
(Ⅱ)T(0,1)
解析:
(Ⅰ)由![]()
因直线![]() 相切,
相切,![]() ,∴
,∴![]() ,
,
…… 2分
∵圆![]() 的两焦点与短轴的一个端点的连线构成等腰直角三角
的两焦点与短轴的一个端点的连线构成等腰直角三角
形,∴![]() …… 4分
…… 4分
故所求椭圆方程为![]() …… 5分
…… 5分
(Ⅱ)当L与x轴平行时,以AB为直径的圆的方程:![]()
当L与x轴垂直时,以AB为直径的圆的方程:![]()
由
即两圆公共点(0,1)
因此,所求的点T如果存在,只能是(0,1) …… 8分
(ⅰ)当直线L斜率不存在时,以AB为直径的圆过点T(0,1)
(ⅱ)若直线L斜率存在时,可设直线L:![]()
由
记点![]() 、
、 …… 10分
…… 10分

![]()
![]()
∴TA⊥TB,
综合(ⅰ)(ⅱ),以AB为直径的圆恒过点T(0,1). …… 12分

练习册系列答案
相关题目
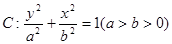 的两焦点与短轴的一个端点连结成等腰直角三角形,直线
的两焦点与短轴的一个端点连结成等腰直角三角形,直线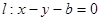 是抛物线
是抛物线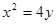 的一条切线。
的一条切线。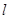 交椭圆
交椭圆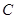 于A、B两点,若点P满足
于A、B两点,若点P满足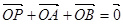 (O为坐标原点), 判断点P是否在椭圆
(O为坐标原点), 判断点P是否在椭圆 的两焦点与短轴的一个端点的连线构成等腰直角三角形,直线
的两焦点与短轴的一个端点的连线构成等腰直角三角形,直线 是抛物线
是抛物线 的一条切线.
的一条切线. 的动直线L交椭圆C于A.B两点.问:是否存在一个定点T,使得以AB为直径的圆恒过点T ? 若存在,求点T坐标;若不存在,说明理由.
的动直线L交椭圆C于A.B两点.问:是否存在一个定点T,使得以AB为直径的圆恒过点T ? 若存在,求点T坐标;若不存在,说明理由.