题目内容
已知正项数列{an}满足a1＝1，(n＋2)an＋12－(n＋1)
＋anan＋1＝0，则它的通项公式为( )．
A．an＝
B．an＝
C．an＝
D．an＝n
B
【解析】由(n＋2)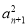
－(n＋1)
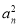＋anan＋1＝0，得(n＋2)·
＋
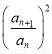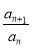＝n＋1，即
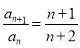，则an＝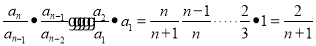
.
练习册系列答案
相关题目
题目内容
已知正项数列{an}满足a1＝1，(n＋2)an＋12－(n＋1)＋anan＋1＝0，则它的通项公式为( )．
A．an＝ B．an＝
C．an＝ D．an＝n
B
【解析】由(n＋2)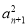－(n＋1)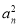＋anan＋1＝0，得(n＋2)·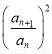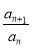＋＝n＋1，即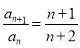，则an＝.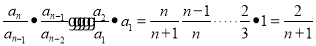
