题目内容
设集合A={x|-1<x<4}, ,C={x|1-2a<x<2a}.
,C={x|1-2a<x<2a}.
(1)若C=∅,求实数a的取值范围;
(2)若C≠∅且C⊆(A∩B),求实数a的取值范围.
解:(1)∵C={x|1-2a<x<2a}=∅,
∴1-2a≥2a,
∴ ,
,
即实数a的取值范围是 .
.
(2)∵C={x|1-2a<x<2a}≠∅,
∴1-2a<2a,即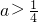
∵A={x|-1<x<4}, ,
,
∴ ,
,
∵C⊆(A∩B)
∴
解得
即实数a的取值范围是 .
.
分析:(1)由C={x|1-2a<x<2a}=∅,得1-2a≥2a,由此能求出实数a的取值范围.
(2)由C={x|1-2a<x<2a}≠∅,得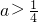 ,由A={x|-1<x<4},
,由A={x|-1<x<4}, ,得
,得 ,由C⊆(A∩B),得
,由C⊆(A∩B),得 ,由此能求出实数a的取值范围.
,由此能求出实数a的取值范围.
点评:本题考查集合的交、并、实集的混合运算,解题时要认真审题,仔细解答,注意不等式知识的合理运用.
∴1-2a≥2a,
∴
 ,
,即实数a的取值范围是
 .
.(2)∵C={x|1-2a<x<2a}≠∅,
∴1-2a<2a,即
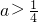
∵A={x|-1<x<4},
 ,
,∴
 ,
,∵C⊆(A∩B)
∴

解得

即实数a的取值范围是
 .
.分析:(1)由C={x|1-2a<x<2a}=∅,得1-2a≥2a,由此能求出实数a的取值范围.
(2)由C={x|1-2a<x<2a}≠∅,得
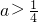 ,由A={x|-1<x<4},
,由A={x|-1<x<4}, ,得
,得 ,由C⊆(A∩B),得
,由C⊆(A∩B),得 ,由此能求出实数a的取值范围.
,由此能求出实数a的取值范围.点评:本题考查集合的交、并、实集的混合运算,解题时要认真审题,仔细解答,注意不等式知识的合理运用.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
设集合A={x|1+log2|x|≤0},B={x|
≤x≤2},则A∩(CRB)=( )
| 1 |
| 4 |
A、[-
| ||||||
B、[-
| ||||||
C、(-∞,-
| ||||||
D、[-
|