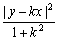题目内容
19.已知k>0,直线l1:y=kx,l2:y=-kx.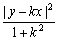
19题图
(Ⅰ)证明:到l1、l2的距离的平方和为定值a(a>0)的点的轨迹是圆或椭圆;
(Ⅱ)求到l1、l2的距离之和为定值c(c>0)的点的轨迹.
19.本小题主要考查直线、圆、椭圆的方程和性质,曲线和方程的关系,轨 迹的概念和求法.利用方程判定曲线的性质等解析几何的基本思想和综 合运用知识的能力.
解: (Ⅰ)设点P(x,y)为动点,则
![]() +
+![]() =a,
=a,
整理得
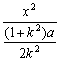 +
+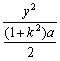 =1.
=1.
因此,当k=1时,动点的轨迹为圆;当k≠1时,动点的轨迹为椭圆.
(Ⅱ)设点P(x,y)为动点,则
|y-kx|+|y+kx|=c![]() .
.
当y≥k|x|时,y-kx+y+kx=c![]() ,即y=
,即y=![]() c
c![]() ;
;
当y≤-k|x|时,kx-y-y-kx=c![]() ,即
,即
y=-![]() c
c![]() ;
;
当-k|x|<y<k|x|,x>0时,kx-y+y+kx=c![]() ,即
,即
x=![]() c
c![]() ;
;
当-k|x|<y<k|x|,x<0时,y-kx-y-kx=c![]() ,即
,即
x=-![]() c
c![]() .
.
综上,动点的轨迹为矩形.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目