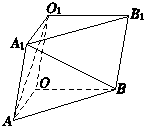
题目内容
如图所示，三棱柱OAB-O1A1B1中，平面OBB1O1⊥平面OAB，∠O1OB=60°，∠AOB=90°，且OB=OO1=2，OA=
，求异面直线A1B与AO1所成角的余弦值的大小．
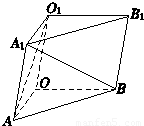
【答案】分析：建立空间直角坐标系，用坐标表示出向量，利用向量的夹角公式，即可求得结论．
解答：
解：建立如图所示的空间直角坐标系，则O（0，0，0），
，
∴
∴cos
=
=
=-
∴异面直线A1B与AO1所成角的余弦值为
．
点评：本题考查线线角，考查向量知识的运用，考查学生的计算能力，属于中档题．
解答：
解：建立如图所示的空间直角坐标系，则O（0，0，0），，∴
∴cos
===-∴异面直线A1B与AO1所成角的余弦值为
．点评：本题考查线线角，考查向量知识的运用，考查学生的计算能力，属于中档题．
练习册系列答案
相关题目
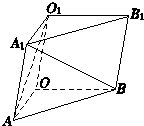如图所示，三棱柱OAB-O1A1B1中，平面OBB1O1⊥平面OAB，∠O1OB=60°，∠AOB=90°，且OB=OO1=2，OA=
已知正三棱柱ABC-A′B′C′的正（主）视图和侧（左）视图如图所示．设△ABC，△A′B′C′的中心分别是O，O′，现将此三棱柱绕直线OO′旋转，射线OA旋转所成的角为x弧度（x可以取到任意一个实数），对应的俯视图的面积为S（x），则函数S（x）的最大值为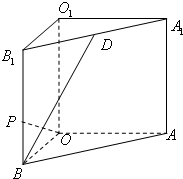
如图所示，在直三棱柱ABO-A1B1O1中，OO1=4，OA=4，OB=3，∠AOB=90°，D是线段A1B1的中点，P是侧棱BB1上的一点．若OP⊥BD，求三棱锥D-OPB的体积．