题目内容
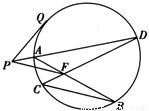
圆的两条弦AB、CD交于点F，从F点引BC的平行线和直线DA的延长线交于点P，再从点P引这个圆的切线，切点是Q．求证：PF=PQ．
分析：首先根据已知题意证明△APF∽△FPD得到PF2=PA•PD；然后通过PQ与圆相切证明PQ2=PA•PD，综合即可证出PF=PQ．
解答：解：∵ABCD四点共线
∴∠ADF=∠ABC
又∵PF∥BC
∴∠AFP=∠FDP
又∵∠CPF=∠FPD
∴△APF∽△FPD
∴
=
∴PF2=PA•PD
又PQ与圆相切
∴PQ2=PA•PD
∴QF2=PQ2
∴PF=PQ
∴∠ADF=∠ABC
又∵PF∥BC
∴∠AFP=∠FDP
又∵∠CPF=∠FPD
∴△APF∽△FPD
∴
| PF |
| PA |
| PD |
| PF |
∴PF2=PA•PD
又PQ与圆相切
∴PQ2=PA•PD
∴QF2=PQ2
∴PF=PQ
点评：本题考查圆的切线的性质定理的证明以及相似三角形的性质，通过圆将直线联系起来，考查了对直线与圆位置关系的灵活运用，属于基础题．
练习册系列答案
阅读快车系列答案
相关题目
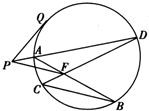圆的两条弦AB、CD交于点F，从F点引BC的平行线和直线DA的延长线交于点P，再从点P引这个圆的切线，切点是Q．
