题目内容
12.已知{an}是等差数列,Sn是其前n项和,S11=$\frac{33}{4}$π,则tana6=-1.分析 由已知结合等差数列的性质求得a6,则答案可求.
解答 解:∵{an}是等差数列,∴S11=$\frac{33}{4}$π=11a6,则${a}_{6}=\frac{3}{4}π$,
∴tana6=tan$\frac{3π}{4}=-1$.
故答案为:-1.
点评 本题考查等差数列的性质,含有奇数项的等差数列中,其前n项和等于中间项乘以项数,是基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
2.若A={a,b,c},则集合A的子集个数是( )
| A. | 3 | B. | 4 | C. | 7 | D. | 8 |
1.如图所示,圆O为正三角形ABC的内切圆,P为圆O上一点,向量$\overrightarrow{AP}$=x$\overrightarrow{AB}$+y$\overrightarrow{AC}$,则x+y的取值范围为( )
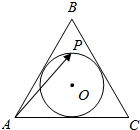

| A. | [$\frac{1}{2}$,1] | B. | [$\frac{1}{3}$,1] | C. | [$\frac{1}{4}$,1] | D. | [$\frac{1}{3}$,$\frac{1}{2}$] |
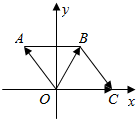 如图已知四边形AOCB中,|$\overrightarrow{OA}$|=5,$\overrightarrow{OC}$=(5,0),点B位于第一象限,若△BOC为正三角形.
如图已知四边形AOCB中,|$\overrightarrow{OA}$|=5,$\overrightarrow{OC}$=(5,0),点B位于第一象限,若△BOC为正三角形.