题目内容
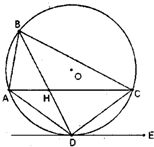已知A、B、C、D为圆O上的四点，直线DE为圆O的切线，AC∥DE，AC与BD相交于H点（Ⅰ）求证：BD平分∠ABC
（Ⅱ）若AB=4，AD=6，BD=8，求AH的长．
分析：（Ⅰ）证明BD平分∠ABC可通过证明D是
的中点，利用相等的弧所对的圆周角相等证明BD是角平分线；
（Ⅱ）由图形知，可先证△ABH∽△DBC，得到
=
，再由等弧所对的弦相等，得到AD=DC，从而得到
=
，求出AH的长
 |
| AC |
（Ⅱ）由图形知，可先证△ABH∽△DBC，得到
| AH |
| CD |
| AB |
| BD |
| AH |
| AD |
| AB |
| BD |
解答：解：（Ⅰ）∵AC∥DE，直线DE为圆O的切线，∴D是弧
的中点，即
=
又∠ABD，∠DBC与分别是两弧
，
所对的圆周角，故有∠ABD=∠DBC，
所以BD平分∠ABC
（Ⅱ）∵由图∠CAB=∠CDB且∠ABD=∠DBC
∴△ABH∽△DBC，∴
=
又
=
∴AD=DC，
∴
=
∵AB=4，AD=6，BD=8
∴AH=3
|
| AC |
|
| AD |
|
| DC |
又∠ABD，∠DBC与分别是两弧
|
| AD |
|
| DC |
所以BD平分∠ABC
（Ⅱ）∵由图∠CAB=∠CDB且∠ABD=∠DBC
∴△ABH∽△DBC，∴
| AH |
| CD |
| AB |
| BD |
又
|
| AD |
|
| DC |
∴AD=DC，
∴
| AH |
| AD |
| AB |
| BD |
∵AB=4，AD=6，BD=8
∴AH=3
点评：本题考查与圆有关的比例线段，解题的关键是对与圆有关性质掌握得比较熟练，能根据这些性质得出角的相等，边的相等，从而使问题得到证明
练习册系列答案
相关题目