题目内容
设函数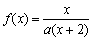 ,方程x=f(x)有唯一解,其中实数a为常数,
,方程x=f(x)有唯一解,其中实数a为常数, ,f(xn)=xn+1(n∈N*)。 (1)求f(x)的表达式;
,f(xn)=xn+1(n∈N*)。 (1)求f(x)的表达式;
(2)求x2011的值;
(3)若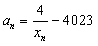 且
且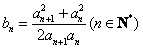 ,求证:
,求证: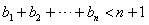 。
。
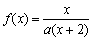 ,方程x=f(x)有唯一解,其中实数a为常数,
,方程x=f(x)有唯一解,其中实数a为常数, ,f(xn)=xn+1(n∈N*)。 (1)求f(x)的表达式;
,f(xn)=xn+1(n∈N*)。 (1)求f(x)的表达式;(2)求x2011的值;
(3)若
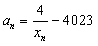 且
且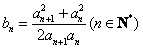 ,求证:
,求证: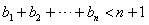 。
。 解:(1)由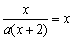 ,可化简为ax(x+2)=x,
,可化简为ax(x+2)=x,
∴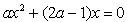 ,
,
当且仅当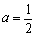 时,方程x=f(x)有唯一解,
时,方程x=f(x)有唯一解,
从而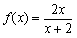 。
。
(2)由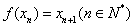 ,得
,得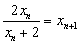 ,
,
∴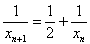 ,即
,即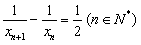 ,
,
∴数列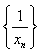 是以
是以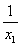 为首项,
为首项, 为公差的等差数列,
为公差的等差数列,
∴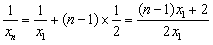 ,即
,即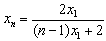 ,
,
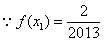 ,
,
∴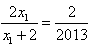 ,解得:
,解得: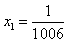 ,
,
∴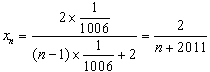 ,
,
故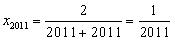 。
。
(3)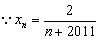 ,
,
∴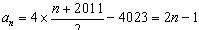 ,
,
∴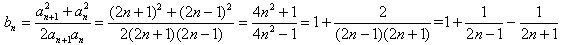 ,
,
∴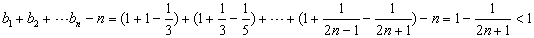 ,
,
故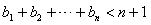 。
。
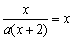 ,可化简为ax(x+2)=x,
,可化简为ax(x+2)=x,∴
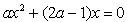 ,
,当且仅当
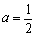 时,方程x=f(x)有唯一解,
时,方程x=f(x)有唯一解,从而
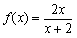 。
。 (2)由
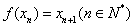 ,得
,得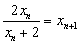 ,
,∴
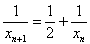 ,即
,即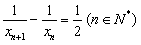 ,
,∴数列
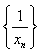 是以
是以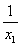 为首项,
为首项, 为公差的等差数列,
为公差的等差数列,∴
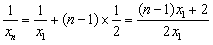 ,即
,即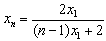 ,
,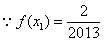 ,
,∴
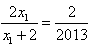 ,解得:
,解得: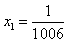 ,
,∴
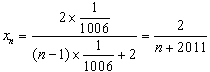 ,
,故
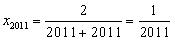 。
。(3)
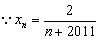 ,
,∴
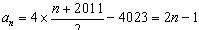 ,
,∴
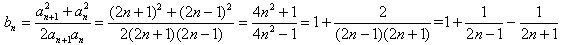 ,
,∴
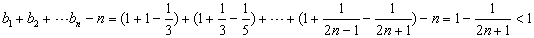 ,
,故
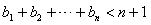 。
。
练习册系列答案
 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案
相关题目
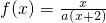 ,方程x=f(x)有唯一解,其中实数a为常数,
,方程x=f(x)有唯一解,其中实数a为常数,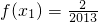 ,f(xn)=xn+1(n∈N*)
,f(xn)=xn+1(n∈N*)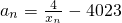 且
且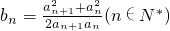 ,求证:b1+b2+…+bn<n+1.
,求证:b1+b2+…+bn<n+1.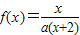 ,方程x=f(x)有唯一解,其中实数a为常数,
,方程x=f(x)有唯一解,其中实数a为常数,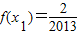 ,f(xn)=xn+1(n∈N*)
,f(xn)=xn+1(n∈N*)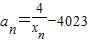 且
且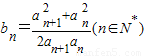 ,求证:b1+b2+…+bn<n+1.
,求证:b1+b2+…+bn<n+1.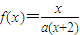 ,方程x=f(x)有唯一解,其中实数a为常数,
,方程x=f(x)有唯一解,其中实数a为常数,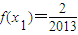 ,f(xn)=xn+1(n∈N*)
,f(xn)=xn+1(n∈N*)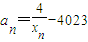 且
且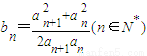 ,求证:b1+b2+…+bn<n+1.
,求证:b1+b2+…+bn<n+1.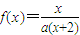 ,方程x=f(x)有唯一解,其中实数a为常数,
,方程x=f(x)有唯一解,其中实数a为常数,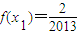 ,f(xn)=xn+1(n∈N*)
,f(xn)=xn+1(n∈N*) 且
且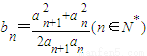 ,求证:b1+b2+…+bn<n+1.
,求证:b1+b2+…+bn<n+1.