题目内容
已知函数f（x）=|sinx|．
（1）若g（x）=ax﹣f（x）≥0对任意x∈[0，+∞）恒成立，求实数a的取值范围；
（2）若函数f（x）=|sinx|的图象与直线y=kx（k＞0）有且仅有三个公共点，且公共点的横坐标的最大值为α，求证：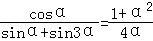
．
（1）若g（x）=ax﹣f（x）≥0对任意x∈[0，+∞）恒成立，求实数a的取值范围；
（2）若函数f（x）=|sinx|的图象与直线y=kx（k＞0）有且仅有三个公共点，且公共点的横坐标的最大值为α，求证：
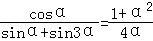．解：（1）根据图象可知，我们只需要考虑
，
此时g（x）=ax﹣sinx
所以g′（x）=a﹣cosx
当a≥1时，g′（x）≥0，易知函数g（x）单调增，
从而g（x）≥g（0）=0，符合题意；
当a≤0，g′（x）＜0，函数g（x）单调减，从而g（x）≤g（0） 不符合题意；
当0＜a＜1时，显然存在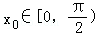
，使得g′（x）=0，且x∈[0，x0）时函数g（x）单调减，
从而g（x）≤g（0）=0，不符合题意．
综上讨论知a≥1．
（2）f（x）的图象与直线y=kx（k＞0）有且仅有三个公共点时如图所示，
且在
内相切，其切点为A（α，﹣sinα），
由于f′（x）=﹣cosx，
，
则
故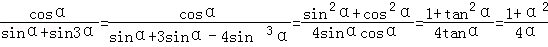
．
，此时g（x）=ax﹣sinx
所以g′（x）=a﹣cosx
当a≥1时，g′（x）≥0，易知函数g（x）单调增，
从而g（x）≥g（0）=0，符合题意；
当a≤0，g′（x）＜0，函数g（x）单调减，从而g（x）≤g（0） 不符合题意；
当0＜a＜1时，显然存在
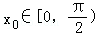，使得g′（x）=0，且x∈[0，x0）时函数g（x）单调减，从而g（x）≤g（0）=0，不符合题意．
综上讨论知a≥1．
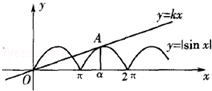
（2）f（x）的图象与直线y=kx（k＞0）有且仅有三个公共点时如图所示，
且在
内相切，其切点为A（α，﹣sinα），由于f′（x）=﹣cosx，
，则
故
．
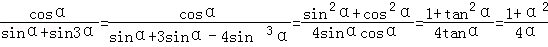练习册系列答案
相关题目
已知函数f（x）=x2-bx的图象在点A（1，f（1））处的切线l与直线3x-y+2=0平行，若数列{
}的前n项和为Sn，则S2010的值为（ ）
| 1 |
| f(n) |
A、
| ||
B、
| ||
C、
| ||
D、
|