题目内容
已知椭圆: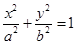 (
( )上任意一点到两焦点距离之和为
)上任意一点到两焦点距离之和为 ,离心率为
,离心率为 ,左、右焦点分别为
,左、右焦点分别为 ,
, ,点
,点 是右准线上任意一点,过
是右准线上任意一点,过 作直 线
作直 线 的垂线
的垂线 交椭圆于
交椭圆于 点.
点.

(1)求椭圆 的标准方程;
的标准方程;
(2)证明:直线 与直线
与直线 的斜率之积是定值;
的斜率之积是定值;
(3)点 的纵坐标为3,过
的纵坐标为3,过 作动直线
作动直线 与椭圆交于两个不同点
与椭圆交于两个不同点 ,在线段
,在线段 上取点
上取点 ,满足
,满足 ,试证明点
,试证明点 恒在一定直线上.
恒在一定直线上.
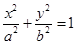 (
( )上任意一点到两焦点距离之和为
)上任意一点到两焦点距离之和为 ,离心率为
,离心率为 ,左、右焦点分别为
,左、右焦点分别为 ,
, ,点
,点 是右准线上任意一点,过
是右准线上任意一点,过 作直 线
作直 线 的垂线
的垂线 交椭圆于
交椭圆于 点.
点.
(1)求椭圆
 的标准方程;
的标准方程;(2)证明:直线
 与直线
与直线 的斜率之积是定值;
的斜率之积是定值;(3)点
 的纵坐标为3,过
的纵坐标为3,过 作动直线
作动直线 与椭圆交于两个不同点
与椭圆交于两个不同点 ,在线段
,在线段 上取点
上取点 ,满足
,满足 ,试证明点
,试证明点 恒在一定直线上.
恒在一定直线上.(1) ;(2)证明详见解析;(3)证明详见解析.
;(2)证明详见解析;(3)证明详见解析.
 ;(2)证明详见解析;(3)证明详见解析.
;(2)证明详见解析;(3)证明详见解析.试题分析:(1)利用椭圆的定义、离心率的定义、
 的关系列出方程组,解得
的关系列出方程组,解得 的值;(2)由右准线方程设出
的值;(2)由右准线方程设出 点坐标,由垂直的充要条件得
点坐标,由垂直的充要条件得 ,表达出
,表达出 ,将
,将 点代入椭圆
点代入椭圆 中,即
中,即 ,代入
,代入 中,化简得常数;(3)设出点
中,化简得常数;(3)设出点 ,代入椭圆方程中,设
,代入椭圆方程中,设 ,由
,由 得向量关系,得到
得向量关系,得到 与
与 的关系,据
的关系,据 与
与 及
及 与
与 系数比为2:3,得
系数比为2:3,得 在直线
在直线 .
.试题解析:(1)由题意可得
 ,解得
,解得 ,
, ,
, ,
,所以椭圆
 :
: . 2分
. 2分(2)由(1)可知:椭圆的右准线方程为
 ,
,设
 ,
,因为PF2⊥F2Q,所以
 ,
,所以
 ,
,又因为
 且
且 代入化简得
代入化简得 .
.即直线
 与直线
与直线 的斜率之积是定值
的斜率之积是定值 . 7分.
. 7分.(3)设过
 的直线l与椭圆交于两个不同点
的直线l与椭圆交于两个不同点 ,点
,点 ,则
,则 ,
, .
.设
 ,则
,则 ,
,∴
 ,
, ,
,整理得
 ,
, ,
, ,
,∴从而
 ,
,由于
 ,
, ,∴我们知道
,∴我们知道 与
与 的系数之比为2:3,
的系数之比为2:3, 与
与 的系数之比为2:3.
的系数之比为2:3.∴
 ,
,所以点
 恒在直线
恒在直线 上. 13分
上. 13分
练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
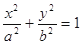 (
(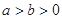 )右顶点与右焦点的距离为
)右顶点与右焦点的距离为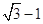 ,短轴长为
,短轴长为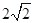 .
.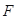 的直线与椭圆分别交于
的直线与椭圆分别交于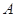 、
、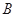 两点,若三角形
两点,若三角形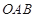 的面积为
的面积为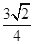 ,求直线
,求直线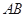 的方程.
的方程. (a>b>0)的两个焦点和短轴的两个端点都在圆
(a>b>0)的两个焦点和短轴的两个端点都在圆 上.
上.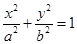 的离心率等于
的离心率等于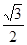 ,点P
,点P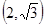 在椭圆上。
在椭圆上。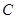 的方程;
的方程;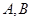 ,过点
,过点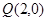 的动直线
的动直线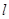 与椭圆
与椭圆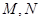 两点,是否存在定直线
两点,是否存在定直线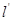 :
: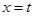 ,使得
,使得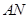 的交点
的交点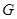 总在直线
总在直线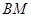 上?若存在,求出一个满足条件的
上?若存在,求出一个满足条件的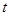 值;若不存在,说明理由.
值;若不存在,说明理由. :
: 的离心率为
的离心率为 ,左焦点为
,左焦点为 .
.  与曲线
与曲线 、
、 两点,且线段
两点,且线段 的中点
的中点 在圆
在圆 上,求
上,求 的值.
的值. 在椭圆
在椭圆 上,F1,F2分别是该椭圆的两焦点,且
上,F1,F2分别是该椭圆的两焦点,且 ,则
,则 的面积是( )
的面积是( )

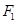 ,
,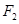 是椭圆的两个焦点,若椭圆上存在点P,使得
是椭圆的两个焦点,若椭圆上存在点P,使得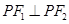 ,则椭圆的离心率的取值范围是( )
,则椭圆的离心率的取值范围是( )



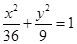 上有两个动点
上有两个动点 、
、 ,
,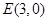 ,
,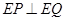 ,则
,则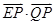 的最小值为( )
的最小值为( )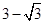
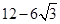
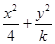 =1的离心率,且e∈(
=1的离心率,且e∈(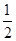 ,1),则实数k的取值范围是 ( )
,1),则实数k的取值范围是 ( ) )
)