题目内容
设 ,则
,则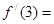 为( )
为( )
A. | B. | C. | D. |
D.
解析试题分析:因为 ,所以
,所以 ,所以
,所以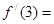
 。
。
考点:本题考查求导公式。
点评:直接应用求导公式计算,属于基础题目。但一定要把求导公式和导数的运算法则记熟。

练习册系列答案
 小学教材全测系列答案
小学教材全测系列答案 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案
相关题目
函数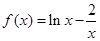 的零点所在的大致区间是( )
的零点所在的大致区间是( )
A.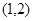 | B.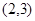 | C.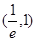 | D.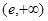 |
函数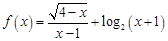 的定义域为( )
的定义域为( )
A.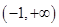 | B.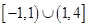 | C.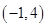 | D.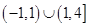 |
若函数
A. | B. |
C. | D. |
设f(x)是R上的奇函数,且当x>0时,f(x)=x(1+ ),则当x<0时,f(x)=( )
),则当x<0时,f(x)=( )
A.-x(1+ ) ) | B.x(1+ ) ) | C.-x(1- ) ) | D. x(1- ) ) |
设函数
 的图象关于直线
的图象关于直线 及直线
及直线 对称,且
对称,且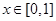 时,
时, ,则
,则 ( )
( )
A. | B. | C. | D. |
已知函数 在区间
在区间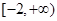 上是增函数,则
上是增函数,则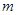 的范围是
的范围是
A.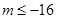 | B. | C.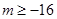 | D.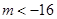 |
 ;②
;② ;③
;③ ;④
;④ .则下列函数图象(在第一象限部分)从左到右依次与函数序号的正确对应顺序是
.则下列函数图象(在第一象限部分)从左到右依次与函数序号的正确对应顺序是 
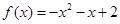 ,则函数
,则函数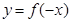 的图象为( )
的图象为( )