题目内容
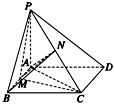
如图所示，已知PA⊥矩形ABCD所在平面，
M，N分别是AB，PC的中点.
（1）求证：MN⊥CD；
（2）若∠PDA=45°.求证：MN⊥平面PCD.
证明略
解析:
（1）连接AC，AN，BN，
∵PA⊥平面ABCD，∴PA⊥AC，
在Rt△PAC中，N为PC中点，
∴AN=
PC.
∵PA⊥平面ABCD，
∴PA⊥BC，又BC⊥AB，PA∩AB=A，
∴BC⊥平面PAB，∴BC⊥PB，
从而在Rt△PBC中，BN为斜边PC上的中线，
∴BN=PC.
∴AN=BN，
∴△ABN为等腰三角形，
又M为底边的中点，∴MN⊥AB，
又∵AB∥CD，∴MN⊥CD.
（2）连接PM、CM,∵∠PDA=45°，PA⊥AD，∴AP=AD.
∵四边形ABCD为矩形.
∴AD=BC，∴PA=BC.
又∵M为AB的中点，∴AM=BM.
而∠PAM=∠CBM=90°,∴PM=CM.
又N为PC的中点，∴MN⊥PC.
由（1）知，MN⊥CD，PC∩CD=C,
∴MN⊥平面PCD.
练习册系列答案
相关题目
22、如图所示，已知PA与⊙O相切，A为切点，PBC为割线，，弦CD∥AP，AD、BC相交于E点，F为CE上一点，且DE2=EF•EC．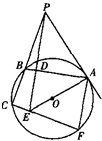
如图所示，已知PA切圆O于A，割线PBC交圆O于B、C，PD⊥AB于D，PD与AO的延长线相交于点E，连接CE并延长交圆O于点F，连接AF．
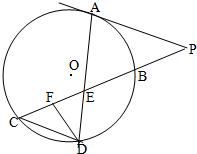如图所示，已知PA与⊙O相切，A为切点，PBC为割线，，弦CD∥AP，AD、BC相交于E点，F为CE上一点，且DE2=EF•EC．
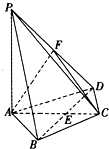如图所示，已知PA⊥平面ABCD，PA=AB=AD=2，AC与BD交于E点，BD=2，BC=CD=
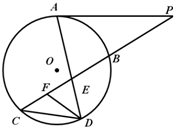（2013•甘肃三模）选修4-1：几何证明选讲