题目内容
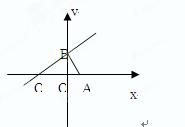
已知 ,点B是
,点B是 轴上的动点,过B作AB的垂线
轴上的动点,过B作AB的垂线 交
交 轴于点Q,若
轴于点Q,若 ,
, .
.

(1)求点P的轨迹方程;
(2)是否存在定直线 ,以PM为直径的圆与直线
,以PM为直径的圆与直线 的相交弦长为定值,若存在,求出定直线方程;若不存在,请说明理由。
的相交弦长为定值,若存在,求出定直线方程;若不存在,请说明理由。
【答案】
(1) y2=x;(2) 存在定直线x=
【解析】
试题分析:(1)设B(0,t),Q(m,0),P(x,y),由射影定理并整理可得m=-4t,然后再利用已知条件 和向量相等的坐标表示的充要条件列出关于x,y的方程即可得到点P的轨迹方程.(2)假设存在.根据已知几何条件和勾股定理列出相交弦的表达式,再寻找a存在的条件即可.
和向量相等的坐标表示的充要条件列出关于x,y的方程即可得到点P的轨迹方程.(2)假设存在.根据已知几何条件和勾股定理列出相交弦的表达式,再寻找a存在的条件即可.
试题解析:(1)设B(0,t),设Q(m,0),t2= |m|,
|m|, m
m 0, m=-4t2,
0, m=-4t2,
 Q(-4t2,0),设P(x,y),则
Q(-4t2,0),设P(x,y),则 =(x-
=(x- ,y),
,y), =(-4t2-
=(-4t2- ,0),
,0),
2 =(-
=(- ,2 t),
,2 t), 
 +
+ =2
=2 。
。
 (x-
(x- ,y)+ (-4t2-
,y)+ (-4t2- ,0)= (-
,0)= (- ,2 t),
,2 t),
 x=4t2,y=2 t,
x=4t2,y=2 t, y2=x,此即点P的轨迹方程;
6分。
y2=x,此即点P的轨迹方程;
6分。
(2)由(1),点P的轨迹方程是y2=x;设P(y2,y), M (4,0) ,则以PM为直径的圆的圆心即PM的中点T(
M (4,0) ,则以PM为直径的圆的圆心即PM的中点T( ,
, ), 以PM为直径的圆与直线x=a的相交弦长:
), 以PM为直径的圆与直线x=a的相交弦长:
L=2
=2 =2
=2 10分
10分
若a为常数,则对于任意实数y,L为定值的条件是a- =0,
即a=
=0,
即a= 时,L=
时,L=
 存在定直线x=
存在定直线x= ,以PM为直径的圆与直线x=
,以PM为直径的圆与直线x= 的相交弦长为定值
的相交弦长为定值 。
。
(2)存在定直线x= ,以PM为直径的圆与直线x=
,以PM为直径的圆与直线x= 的相交弦长为定值
的相交弦长为定值
考点:1.射影定理;2.向量相等的坐标表示的充要条件;3.勾股定理.

练习册系列答案
相关题目
 ,点B是
,点B是 轴上的动点,过B作AB的垂线
轴上的动点,过B作AB的垂线 交
交 轴于点Q,若
轴于点Q,若 ,
, .
.
 ,以PM为直径的圆与直线
,以PM为直径的圆与直线 ,点B是
,点B是 轴上的动点,过B作AB的垂线
轴上的动点,过B作AB的垂线 交
交 轴于点Q,若
轴于点Q,若 ,
, .
.
 ,以PM为直径的圆与直线
,以PM为直径的圆与直线 ,点B是
,点B是 轴上的动点,过B作AB的垂线
轴上的动点,过B作AB的垂线 交
交 轴于点Q,若
轴于点Q,若 ,
, .
.
 ,以PM为直径的圆与直线
,以PM为直径的圆与直线