题目内容
某地区预计明年从年初开始的前x个月内,对某种商品的需求总量f(x)(万件)与月份x的近似关系为
f(x)= x(x+1)(35-2x)(x∈N且x≤12),
x(x+1)(35-2x)(x∈N且x≤12),
(1)写出明年第x个月的需求量g(x)(万件)与月份x的函数关系式,并求出哪个月份的需求量超过1.4万件;
(2)如果将该商品每月都投放市场p万件,要保持每月都满足市场需求,则p至少为多少万件。
f(x)=
 x(x+1)(35-2x)(x∈N且x≤12),
x(x+1)(35-2x)(x∈N且x≤12),(1)写出明年第x个月的需求量g(x)(万件)与月份x的函数关系式,并求出哪个月份的需求量超过1.4万件;
(2)如果将该商品每月都投放市场p万件,要保持每月都满足市场需求,则p至少为多少万件。
解:(1)由题设条件知 (x∈N且x≤12),
(x∈N且x≤12),
令 ,
,
整理得 ,
,
∴5<x<7,
又x∈N,
∴x=6,
即6月份的需求量超过1.4万件;
(2)为满足市场需求,
则 ,
,
∵g(x)的最大值为 ,
,
∴p≥ ,即p至少为
,即p至少为 万件。
万件。
 (x∈N且x≤12),
(x∈N且x≤12), 令
 ,
,整理得
 ,
,∴5<x<7,
又x∈N,
∴x=6,
即6月份的需求量超过1.4万件;
(2)为满足市场需求,
则
 ,
,∵g(x)的最大值为
 ,
,∴p≥
 ,即p至少为
,即p至少为 万件。
万件。
练习册系列答案
 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案
相关题目
 x(x+1)(35-2x)(x∈N*,且x≤12).
x(x+1)(35-2x)(x∈N*,且x≤12).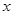 个月内,对某种商品的需求总量
个月内,对某种商品的需求总量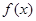 (万件)与月份
(万件)与月份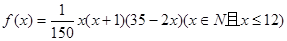 .
.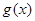 (万件)与月份
(万件)与月份