题目内容
已知函数f（x）定义域为（0，+∞），且满足2f（x）+f（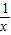
）=（2x-
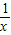）lnx．（Ⅰ）求f（x）解析式及最小值；
（Ⅱ）设g（x）=
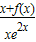，h（x）=（2x2+x）g′（x），求证：?x∈（0，+∞），h（x）＜
．
【答案】分析：（1）令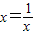
，构建关于f（x）与
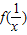的方程组，可求得结果．利用导数有关知识即能求得函数的最小值；
（2）利用导数研究函数h（x）在（0，+∞）上的最大值，就能证得结果．
解答：（1）解：令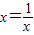
，代入2f（x）+f（
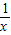）=（2x-
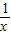）lnx ①
得，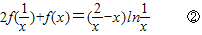
联立①②解得：f（x）=xlnx
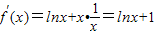
当x∈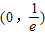
时，f′（x）0，函数递增．
∴当x=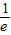
时，函数取到极小值，也是函数的最小值
故最小值为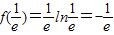
（2）证明：由（1）得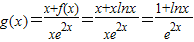
∴
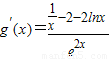
∴h（x）=（2x2+x）g′（x）=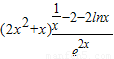
=
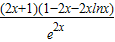
令p（x）=1-2x-2xlnx
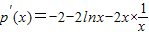=-4-2lnx
当x∈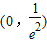
时，p′（x）＞0，函数递增；当x∈
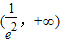时，p′（x）＜0，函数递减．
故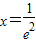
时，函数取到极大值，也是函数的最大值．
即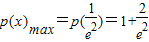
，且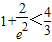
同理可求得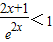
故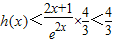
点评：本题主要考查了函数解析式的求法、利用导数研究函数的最值；解题中要熟悉复杂函数的求导；对运算的要求比较高．
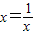，构建关于f（x）与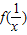的方程组，可求得结果．利用导数有关知识即能求得函数的最小值；（2）利用导数研究函数h（x）在（0，+∞）上的最大值，就能证得结果．
解答：（1）解：令
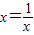，代入2f（x）+f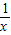（）=（2x-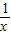）lnx ①得，
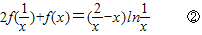
联立①②解得：f（x）=xlnx
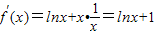
当x∈
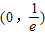时，f′（x）0，函数递增．∴当x=
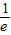时，函数取到极小值，也是函数的最小值故最小值为
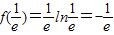
（2）证明：由（1）得
∴
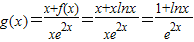
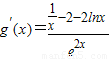
∴h（x）=（2x2+x）g′（x）=
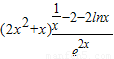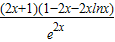
=令p（x）=1-2x-2xlnx
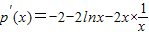=-4-2lnx当x∈
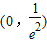时，p′（x）＞0，函数递增；当x∈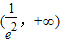时，p′（x）＜0，函数递减．故
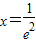时，函数取到极大值，也是函数的最大值．即
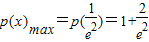，且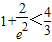同理可求得
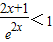
故
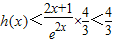
点评：本题主要考查了函数解析式的求法、利用导数研究函数的最值；解题中要熟悉复杂函数的求导；对运算的要求比较高．
练习册系列答案
相关题目