题目内容
(1)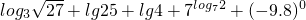
(2)已知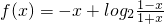 .求
.求 的值.
的值.
解:(1)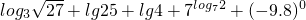
=
=
=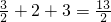 ;
;
(2)由 得:-1<x<1.所以f(x)的定义域为:(-1,1),
得:-1<x<1.所以f(x)的定义域为:(-1,1),
又 =
= ,
,
所以f(x)为奇函数,所以 =0.
=0.
分析:(1)化根式为分数指数幂,然后利用对数式的运算性质化简求值;
(2)求出函数的定义域,定义域关于原点对称,然后判断出函数式奇函数,利用基函数的性质得答案.
点评:本题考查了对数式的运算性质,考查了基函数的性质,解答此题(2)的关键在于判断函数f(x)的奇偶性,是基础题.
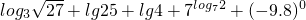
=

=

=
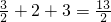 ;
;(2)由
 得:-1<x<1.所以f(x)的定义域为:(-1,1),
得:-1<x<1.所以f(x)的定义域为:(-1,1),又
 =
= ,
,所以f(x)为奇函数,所以
 =0.
=0.分析:(1)化根式为分数指数幂,然后利用对数式的运算性质化简求值;
(2)求出函数的定义域,定义域关于原点对称,然后判断出函数式奇函数,利用基函数的性质得答案.
点评:本题考查了对数式的运算性质,考查了基函数的性质,解答此题(2)的关键在于判断函数f(x)的奇偶性,是基础题.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目

 ,求f(x)的解析式
,求f(x)的解析式
 ,求
,求 的值.
的值. 
 ,求
,求 的值。
的值。 ;
;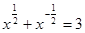 ,求
,求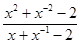 的值.
的值.
 ,求
,求 的值。
的值。