题目内容
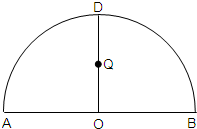 如图,ADB为半圆,AB为半圆直径,O为半圆圆心,且OD⊥AB,Q为线段OD的中点,已知|AB|=4,曲线C过Q点,动点P在曲线C上运动且保持|PA|+|PB|的值不变
如图,ADB为半圆,AB为半圆直径,O为半圆圆心,且OD⊥AB,Q为线段OD的中点,已知|AB|=4,曲线C过Q点,动点P在曲线C上运动且保持|PA|+|PB|的值不变(1)建立适当的平面直角坐标系,求曲线C的方程;
(2)过D点的直线l与曲线C相交于不同的两点M、N,且M在D、N之间,设
| |DM| | |DN| |
分析:(1)以AB、OD所在直线分别为x轴、y轴,O为原点,建立平面直角坐标系,由已知条件判断该曲线为椭圆,由所给条件易求a,b,c值;
(2)分两种情况进行讨论:直线存在斜率k时,设直线方程,与椭圆联立方程组,根据判别式可求得k的范围,用韦达定理及
=λ可得λ与k的关系式,借助k的范围即可求得λ范围,注意M点位于中间;当直线不存在斜率k时,易求λ值,综上即可求得范围.
(2)分两种情况进行讨论:直线存在斜率k时,设直线方程,与椭圆联立方程组,根据判别式可求得k的范围,用韦达定理及
| |DM| |
| |DN| |
解答: 解 (1)以AB、OD所在直线分别为x轴、y轴,O为原点,建立平面直角坐标系,?
解 (1)以AB、OD所在直线分别为x轴、y轴,O为原点,建立平面直角坐标系,?
∵|PA|+|PB|=|QA|+|QB|=2
=2
>|AB|=4,
∴曲线C为以原点为中心,A、B为焦点的椭圆,设其长半轴为a,短半轴为b,半焦距为c,则2a=2
,
∴a=
,c=2,b=1,∴曲线C的方程为
+y2=1;
(2)当直线存在斜率时,设直线l的方程为y=kx+2,代入
+y2=1,
得(1+5k2)x2+20kx+15=0,△=(20k)2-4×15(1+5k2)>0,得k2>
,
由图可知
=
=λ,由韦达定理得
,
将x1=λx2代入得
,
两式相除得
=
=
∵k2>
,
∴0<
<
,∴5<
+5<
,∴4<
<
,即4<
<
,
∴解得
<λ<3,∵λ=
=
,M在D、N之间,∴λ<1,
当直线不存在斜率时,易知λ=
=
(此时直线与y轴重合),
综上,
≤λ<1..
 解 (1)以AB、OD所在直线分别为x轴、y轴,O为原点,建立平面直角坐标系,?
解 (1)以AB、OD所在直线分别为x轴、y轴,O为原点,建立平面直角坐标系,?∵|PA|+|PB|=|QA|+|QB|=2
| 22+12 |
| 5 |
∴曲线C为以原点为中心,A、B为焦点的椭圆,设其长半轴为a,短半轴为b,半焦距为c,则2a=2
| 5 |
∴a=
| 5 |
| x2 |
| 5 |
(2)当直线存在斜率时,设直线l的方程为y=kx+2,代入
| x2 |
| 5 |
得(1+5k2)x2+20kx+15=0,△=(20k)2-4×15(1+5k2)>0,得k2>
| 3 |
| 5 |
由图可知
| DM |
| DN |
| x1 |
| x2 |
|
将x1=λx2代入得
|
两式相除得
| (1+λ)2 |
| λ |
| 400k2 |
| 15(1+5k2) |
| 80 | ||
3(5+
|
| 3 |
| 5 |
∴0<
| 1 |
| k2 |
| 5 |
| 3 |
| 1 |
| k2 |
| 20 |
| 3 |
| 80 | ||
3(5+
|
| 16 |
| 3 |
| (1+λ)2 |
| λ |
| 16 |
| 3 |
∴解得
| 1 |
| 3 |
| x1 |
| x2 |
| DM |
| DN |
当直线不存在斜率时,易知λ=
| DM |
| DN |
| 1 |
| 3 |
综上,
| 1 |
| 3 |
点评:本题考查直线与圆锥曲线的位置关系、椭圆标准方程的求解,考查分类讨论思想,考查学生综合运用知识分析问题解决问题的能力,难度较大.

练习册系列答案
相关题目
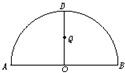 如图,
如图,
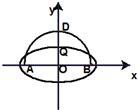 如图,ADB为半圆,AB为直径,O为圆心,
如图,ADB为半圆,AB为直径,O为圆心,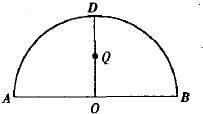 如图,
如图,