Question

某厂使用两种零件A、B装配两种产品X、Y,该厂的生产能力是月产X最多2 500件,月产Y最多1 200件,而组装一件X需要4个A、2个B,组装一件Y需6个A、8个B.某个月,该厂能用A最多14 000个,B最多12 000个,已知产品X每件利润1 000元,产品Y每件利润2 000元,欲使该月利润最高,需组装产品X、Y各多少件?最高利润为多少万元?

Answer 1

解:设月生产产品X、Y分别为x件、y件,该月产品利润为z,

    则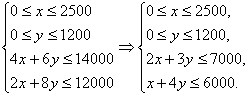

    目标函数z=1 000x+2 000y,即z=1 000(x+2y).

    设x+2y=λ(2x+3y)+k(x+4y),易得λ=,k=.

∴x+2y=(2x+3y)+(x+4y)≤×7 000+×6 000=4 000.

∴z_max=1 000×4 000=4 000 000元=400(万元).

    等号成立的条件是即

    故组装X产品2 000件,Y产品1 000件时,月利润最高,最高利润为400万元.