题目内容
（本小题满分8分）一货轮航行到M处，测得灯塔S在货轮的北偏东15°相距20里处，随后货轮按北偏西30°的方向航行，半小时后，又测得灯塔在货轮的北偏东45°，求货轮的速度。
【答案】
解：如图所示，∠SMN=15°+30°=45°，
∠SNM=180°－45°－30°=105°∴∠NSM=180°－45°－105°=30°
答：货轮的速度为
里/小时
【解析】略
练习册系列答案
相关题目
（本小题满分12分）一名高二学生盼望进入某名牌大学学习，不放弃能考入该大学的任何一次机会。已知该大学通过以下任何一种方式都可被录取：
① 2010年2月国家数学奥赛集训队考试通过（集训队从2009年10月省数学竞赛壹等奖获得者中选拔，通过考试进入集训队则能被该大学提前录取）；
② 2010年3月自主招生考试通过并且2010年6月高考分数达重点线；
③ 2010年6月高考达到该校录取分数线（该校录取分数线高于重点线）。
该名考生竞赛获省一等奖、自主招生考试通过、高考达重点线、高考达该校分数线等事件的概率如下表：
| 事件 | 省数学竞获一等奖 | 自主招生考试通过 | 高考达重点线 | 高考达该校分数线 |
| 概率 | 0.5 | 0.7 | 0.8 | 0.6 |
如果数学竞赛获省一等奖，该学生估计自己进入国家集训队的概率是0.4。
（1）求该学生参加自主招生考试的概率；
（2）求该学生参加考试次数的分布列与数学期望；
（3）求该学生被该大学录取的概率。
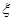的数学期望（用分数表示，精确到0.01）．
名男生、
名女生站成一排照相．(用数字作答)