题目内容
在△ABC中，三角A，B，C所对的边分别为a，b，c．已知△ABC的周长为
+1，且sinA+sinB=
sinC．
（Ⅰ）求边c的长；
（Ⅱ）若△ABC的面积为
sinC，求角C的大小．
| 2 |
| 2 |
（Ⅰ）求边c的长；
（Ⅱ）若△ABC的面积为
| 1 |
| 6 |
（I）由题意及正弦定理，得a+b+c=
+1，（2分）a+b=
c，（4分）
两式相减，得c=1．（6分）
（II）由△ABC的面积
a•b•sinC=
sinC，得a•b=
，（9分）
由余弦定理，得cosC=
=
=
，（12分）
所以C=60°．（14分）
| 2 |
| 2 |
两式相减，得c=1．（6分）
（II）由△ABC的面积
| 1 |
| 2 |
| 1 |
| 6 |
| 1 |
| 3 |
由余弦定理，得cosC=
| a2+b2-c2 |
| 2a•b |
| (a+b)2-2a•b-c2 |
| 2a•b |
| 1 |
| 2 |
所以C=60°．（14分）
练习册系列答案
相关题目
x+2=0的两根，且2cos （A+B）=-1．
,其中a、b是方程x2－2
x＋2＝0的两根，且2cos(A＋B )＝1.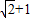
，且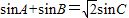
．
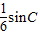，求角C的大小．