题目内容
已知函数f(x)=sin2x+acosx-
 ,x∈R.
,x∈R.
(1)当a=1时,求函数f(x)的最小值;
(2)对于任意x ,不等式f(x)
,不等式f(x) -
- 都成立,求实数a的范围.
都成立,求实数a的范围.
解:(1)当a=1时,f(x)=sin2x+cosx-2=-cos2x+cosx-1=-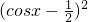 -
- ,
,
因为-1≤cosx≤1,
所以当cosx=-1时f(x)取得最小值,为-3.
(2)f(x)=sin2x+acosx-
 =-cos2x+acosx-
=-cos2x+acosx- a-
a- =-
=- +
+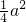 -
-
 ,
,
令t=cosx,由x ,得t∈[
,得t∈[ ,1],
,1],
则g(t)=- ,
,
对于任意x ,不等式f(x)
,不等式f(x) -
- 都成立,
都成立,
则当 ≤
≤ 即a
即a 时,g(t)min=g(1)=
时,g(t)min=g(1)= ≥
≥ -
- ,解得a≥2,与a
,解得a≥2,与a 矛盾;
矛盾;
当 >
> 即a>
即a> 时,g(t)min=g(
时,g(t)min=g( )=-
)=- ≥
≥ -
- ,解得a
,解得a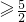 ,所以a
,所以a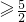 ;
;
综上,实数a的取值范围为a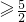 .
.
分析:(1)当a=1时,对f(x)进行配方,根据二次函数的性质即可求得其最小值;
(2)令t=cosx,t∈[ ,1],则f(x)可转化为关于t的二次函数,根据二次函数的性质按a的取值范围进行讨论求得该二次函数的最小值,令最小值大于等于
,1],则f(x)可转化为关于t的二次函数,根据二次函数的性质按a的取值范围进行讨论求得该二次函数的最小值,令最小值大于等于 -
- 解出a即可;
解出a即可;
点评:本题考查二次函数在闭区间上的最值,考查余弦函数的值域,考查函数恒成立,考查转化思想、分类讨论思想,恒成立问题往往转化为函数的最值解决.
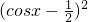 -
- ,
,因为-1≤cosx≤1,
所以当cosx=-1时f(x)取得最小值,为-3.
(2)f(x)=sin2x+acosx-

 =-cos2x+acosx-
=-cos2x+acosx- a-
a- =-
=- +
+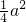 -
-
 ,
,令t=cosx,由x
 ,得t∈[
,得t∈[ ,1],
,1],则g(t)=-
 ,
,对于任意x
 ,不等式f(x)
,不等式f(x) -
- 都成立,
都成立,则当
 ≤
≤ 即a
即a 时,g(t)min=g(1)=
时,g(t)min=g(1)= ≥
≥ -
- ,解得a≥2,与a
,解得a≥2,与a 矛盾;
矛盾;当
 >
> 即a>
即a> 时,g(t)min=g(
时,g(t)min=g( )=-
)=- ≥
≥ -
- ,解得a
,解得a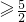 ,所以a
,所以a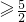 ;
;综上,实数a的取值范围为a
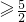 .
.分析:(1)当a=1时,对f(x)进行配方,根据二次函数的性质即可求得其最小值;
(2)令t=cosx,t∈[
 ,1],则f(x)可转化为关于t的二次函数,根据二次函数的性质按a的取值范围进行讨论求得该二次函数的最小值,令最小值大于等于
,1],则f(x)可转化为关于t的二次函数,根据二次函数的性质按a的取值范围进行讨论求得该二次函数的最小值,令最小值大于等于 -
- 解出a即可;
解出a即可;点评:本题考查二次函数在闭区间上的最值,考查余弦函数的值域,考查函数恒成立,考查转化思想、分类讨论思想,恒成立问题往往转化为函数的最值解决.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
