题目内容
(本题16分)
已知函数![]() ,其中
,其中![]() ,
,![]() .
.
(1)当![]() 时,讨论函数
时,讨论函数![]() 的单调性;
的单调性;
(2)若函数![]() 仅在
仅在![]() 处有极值,求
处有极值,求![]() 的取值范围;
的取值范围;
(3)若对于任意的![]() ,不等式
,不等式![]() 在
在![]() 上恒成立,求
上恒成立,求![]() 的取值范围.
的取值范围.
(1)![]() . ……1分
. ……1分
当![]() 时,
时,![]() .令
.令![]() ,解得
,解得![]() ,
,![]() . ……2分
. ……2分
当![]() 变化时,
变化时,![]() ,
,![]() 的变化情况如下表:
的变化情况如下表:
|
|
| 0 |
|
|
|
|
| - | 0 | + | 0 | - |
|
| ↘ | 极小值 | ↗ | 极大值 | ↘ |
所以![]() 在
在![]() 内是增函数,在
内是增函数,在![]() ,
,![]() 内是减函数. ……5分
内是减函数. ……5分
(2)![]() ,显然
,显然![]() 不是方程
不是方程![]() 的根.……7分
的根.……7分
为使![]() 仅在
仅在![]() 处有极值,必须
处有极值,必须![]() 成立, ……8分
成立, ……8分
即有![]() .解不等式,得
.解不等式,得![]() .这时,
.这时,![]() 是唯一极值. ……9分
是唯一极值. ……9分
因此满足条件的![]() 的取值范围是
的取值范围是![]() . ……10分
. ……10分
(3)![]() 由条件
由条件![]() ,可知
,可知![]() , ……11分
, ……11分
从而![]() 恒成立.在
恒成立.在![]() 上,当
上,当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() .
.
因此函数![]() 在
在![]() 上的最大值是
上的最大值是![]() 与
与![]() 两者中的较大者. ……13分
两者中的较大者. ……13分
为使对任意的![]() ,不等式
,不等式![]() 在
在![]() 上恒成立,当且仅当
上恒成立,当且仅当![]() ,即
,即![]() ,在
,在![]() 上恒成立. ……15分
上恒成立. ……15分
所以![]() ,因此满足条件的
,因此满足条件的![]() 的取值范围是
的取值范围是![]() ……16分
……16分

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案
相关题目
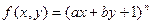 (常数
(常数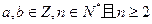 )
)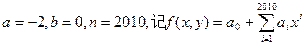 求:①
求:①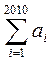 ;②
;②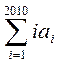
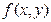 展开式中不含x的项的系数的绝对值之和为729,不含y项的系数的绝对值之和为64,求n的所有可能值。
展开式中不含x的项的系数的绝对值之和为729,不含y项的系数的绝对值之和为64,求n的所有可能值。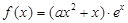 ,其中e是自然数的底数,
,其中e是自然数的底数,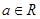 ,
,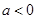 时,解不等式
时,解不等式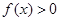 ;
;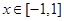 时,不等式
时,不等式 恒成立,求a的取值范围;
恒成立,求a的取值范围;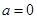 时,试判断:是否存在整数k,使得方程
时,试判断:是否存在整数k,使得方程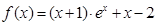 在
在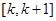
 在定义域
在定义域 上是奇函数,(其中
上是奇函数,(其中 且
且 ).
). 的值,并求出定义域
的值,并求出定义域 在
在 上的单调性,并用定义加以证明;
上的单调性,并用定义加以证明; 时,
时, 及
及 的值.
的值. 的最大值为
的最大值为 ,最小值为
,最小值为 .
. 的值;
的值; 的最小值并求出对应x的集合.
的最小值并求出对应x的集合.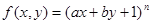 (常数
(常数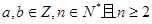 )
)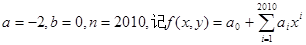 求:①
求:①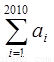 ;②
;②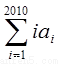
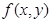 展开式中不含x的项的系数的绝对值之和为729,不含y项的系数的绝对值之和为64,求n的所有可能值。
展开式中不含x的项的系数的绝对值之和为729,不含y项的系数的绝对值之和为64,求n的所有可能值。