题目内容
（本小题满分12分）
如图，在直四棱柱
中，
，
，
，
为
中点，点
在
上.
(1)试确定点的位置，使
；
(2)当时，求二面角
的正切值.
解法一：（1）连结AM，AC，B1M，AB＝BC，∠ABC＝60°⇒△ABC为正三角形.
⇒MN⊥面AB1M⇒MN⊥B1M.…………3分
⇒⇒＝＝⇒NC＝.
即点N的位置在线段CC1的四等分点且靠近C处. ………………………6分
(2)过M作ME⊥AB1于E，连NE.由(1)知MN⊥面AB1M，∴NE⊥AB1(三垂线定理).
∴∠MEN为二面角M—AB1—N的平面角. ………………9分
MN＝＝，AM＝·2＝，B1M＝，AB1＝2.
在Rt△AB1M中，ME＝＝.
在Rt△EMN中，tan∠MEN＝＝.
∴二面角M—AB1—N的正切值为. ……………………12分
解法二：(1)分别以BC，BB1所在直线为
轴，过B且与BC垂直的直线为
轴，建立空间直角坐标系，则
.
.即点N所在位置在比线段CC1的四等分点且靠近C点处.
(2) 设
是平面NAB1的一个法向量
，则
，
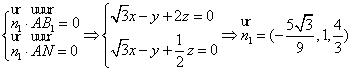同理可得平面MAB1的法向量 
，
，所以二面角
M—AB1—N的正切值为.
练习册系列答案
相关题目
，且
。①求
的最大值及最小值；②求
、
、
.现有3名工人独立地从中任选一个项目参与建设.求：
