题目内容
设变量x，y满足约束条件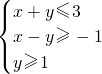
则目标函数z=4x+2y的最大值为
- A.12
- B.10
- C.8
- D.2
B
分析：1．作出可行域 2目标函数z的几何意义：直线截距2倍，直线截距去的最大值时z也取得最大值
解答：本题主要考查目标函数最值的求法，属于容易题，做出可行域，由图可知，当目标函数过直线y=1与x+y=3的交点（2，1）时，z取得最大值10．
点评：本题考查线性规划问题：目标函数的几何意义
分析：1．作出可行域 2目标函数z的几何意义：直线截距2倍，直线截距去的最大值时z也取得最大值
解答：本题主要考查目标函数最值的求法，属于容易题，做出可行域，由图可知，当目标函数过直线y=1与x+y=3的交点（2，1）时，z取得最大值10．
点评：本题考查线性规划问题：目标函数的几何意义
练习册系列答案
相关题目
设变量x，y满足约束条件
，则目标函数u=x2+y2的最大值M与最小值N的比
=（ ）
|
| M |
| N |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|