题目内容
如图为函数，f(x)=Asin(
＞0,K≠0,
＞0,
＜
)的图象的一部分
(Ⅰ)求f(x)的解析式及f(x)的单调递增区间；
(Ⅱ)求f(1)+f (2)+f(3)+…f(2008)的值
解：(I)由图象可知：A=
=1, k=
=1
=3-1=2 ∴T=4 ∴W=
∴f(x)=sin(
x+
∵图像过点（0，1） ∴1= sin
+1 ∴sin=0
∴f(x)=sinx+1
由一+2k
≤x≤+2k (k∈ǎz)得，f(x)的单调递增区间为[一1+4k，l+4k](k∈z)
(Ⅱ)∵f(x)=sin x+l的周期T＝4
又，f(1)=1+1=2 ，f(2)=0+1=1 ，f(3)=-1+1=0 _f(4)=0+1=1
∴f(1)+f(2)+f(3)+lf(4)=2十l+0十1=4
即f(1)+f(2)+f3)+…+f(2008)=502×4=2008
练习册系列答案
相关题目
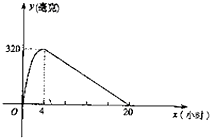某种新药服用x小时后血液中的残留量为y毫克，如图为函数y=f（x）的图象，在x∈（0，4]时为二次函数，且当x=4时到达顶点；在x∈（4，20]为一次函数，当血液中药物残留量不小于240毫克时，治疗有效．
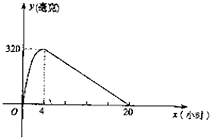某种新药服用x小时后血液中的残留量为y毫克，如图为函数y=f（x）的图象，当血液中药物残留量不小于240毫克时，治疗有效．
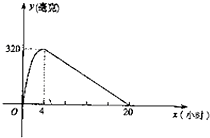某种新药服用x小时后血液中的残留量为y毫克，如图为函数y=f（x）的图象，当血液中药物残留量不小于240毫克时，治疗有效．
(4)的值为( )