Question

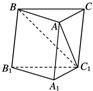
如图所示，斜三棱柱ABC―A₁B₁C₁中，A₁C⊥底面ABC，∠A_lAC=60°,∠BAC=90°，AB=AC=．

(1)求点C_l到平面A_lABB_l的距离；

(2)求二面角A―BC―B₁的正切值．

Answer 1

解：(1)∵A_lC⊥平面ABC，A_lC⊥平面A_lACC_l，

    ∴平面A₁ACC_l⊥平面ABC．

    其中AC为交线，又∠BAC=90°．即AB⊥AC．

    ∴AB⊥平面A₁ACC₁，而AB平面A₁ABB₁，

∴平面A₁ABB_l⊥平面A₁ACC₁，其中A₁A为交线，

由棱柱的性质知C₁C∥平面A₁ABB₁，

    ∴点C₁到平面A₁ABB₁的距离等于点C到平面A₁ABB₁的距离．

    作CM⊥A₁A于M，则CM⊥平面A_lABB₁，

    ∴CM之长就是点C₁到平面A₁ABB₁的距离．

在Rt△ACM中，∠MAC=∠A_lAC=60°，AC=．

∴CM=sin60°=，即点C_l到平面A₁ABB_l的距离为．

(2)作B_lH上平面ABC，H为垂足，连接BH，则有A_lCB_lH，

∴CHA_lB_l，又ABA_lB_l．

    ∴ABCH，而∠BAC=90°，∴四边形ABHC是正方形．

连接AH交BC于O，则AH⊥BC，连接O，则有BC⊥OB₁(三垂线定理)，

∴∠AOB₁是二面角A―BC―B_l的平面角．

在Rt△B_lOH中，B_lH=A_lC=ACtan60°=，

OH=AH=．∴tan∠B_lOH=

    即二面角A―BC―B_l的正切值为－．