题目内容
已知函数f(x)=ax3+bx2+cx+d是R上的奇函数,且在x=1时取得极小值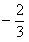 .
.
(1)求函数f(x)的解析式;
(2)对任意x1,x2∈[-1,1],证明: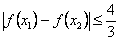 .
.
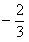 .
. (1)求函数f(x)的解析式;
(2)对任意x1,x2∈[-1,1],证明:
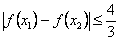 .
. 解:(1)由f(x)是奇函数,可知b=d=0,
所以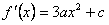 ,
,
可知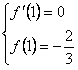
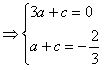
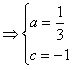 ,
,
所以,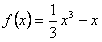 。
。
(2)即证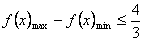 ,
,
因为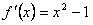 ,所以x∈[-1,1]时,
,所以x∈[-1,1]时,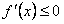 ,从而函数f(x)在[-1,1]上单调递减,
,从而函数f(x)在[-1,1]上单调递减,
所以,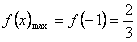 ,
,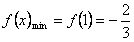 ,
,
所以,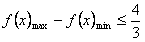 ,
,
从而对任意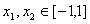 ,有
,有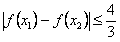 。
。

练习册系列答案
相关题目
已知函数f(x)=a-
,若f(x)为奇函数,则a=( )
| 1 |
| 2x+1 |
A、
| ||
| B、2 | ||
C、
| ||
| D、3 |