题目内容
一个车间为了规定工时定额，需要确定加工零件所花费的时间，为此进行了8次试验，收集数据如下：
| 零件个数x（个） | 10 | 20 | 30 | 40 | 50 | 60 | 70 | 80 |
| 加工时间y（分钟） | 62 | 68 | 75 | 81 | 89 | 95 | 102 | 108 |
，则点
在直线
的（ ）A、右上方 B、右下方 C、左上方 D、左下方
A
解析试题分析：利用线性回归系数公式求出a，b的值，从而可确定点（a，b）与在直线x+45y-20=0的位置关系．根据题意可知
，故可知在直线的上方，故选A.
考点：线性回归系数
点评：本题考查线性回归系数的确定，考查线性规划，解题的关键是确定线性回归系数．
练习册系列答案
字词句篇与同步作文达标系列答案
相关题目
在2013年3月15日，某市物价部门对本市的5家商场的某商品的一天销售量及其价格进行调查，5家商场的售价x元和销售量y件之间的一组数据如下表所示：
| 价格x | 9 | 9.5 | 10 | 10.5 | 11 |
| 销售量y | 11 | 10 | 8 | 6 | 5 |
，那么
的值为 ( )A．－24 B．35.6 C．40.5 D．40
在某次测量中得到的A样本数据如下：82,84,84,86,86,86,88,88,88,88.若B样本数据 恰好是A样本数据都加2后所得数据，则A，B两样本的下列数字特征对应相同的是
| A．众数 | B．平均数 | C．中位数 | D．标准差 |
在两个变量y与x的回归模型中，分别选择了4个不同模型，它们的
如下，其中拟合效果最好的模型是（ ）
| A．模型1的为0.975 | B．模型2的为0.79 |
| C．模型3的为0.55 | D．模型4的为0.25 |
某班50名学生其中考试数学成绩的频率分布直方图如图所示.其中成绩分组区间是：
，
， 
，
，
.则图中
的值为（ ）
| A．0.18 | B．0.018 | C．0.36 | D．0.009 |
统计某校1000名学生的数学水平测试成绩，得到样本频率分布直方图如图所示，若满分为100分，规定不低于60分为及格，则及格率是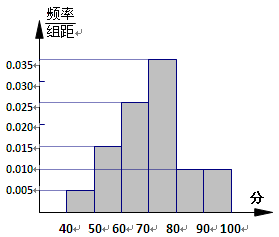
| A．20% |
| B．25% |
| C．6% |
| D．80% |
一个样本a,3,5,7的平均数是b，且a、b是方程x2－5x＋4＝0的两根，则这个样本的方差是( )
| A．3 | B．4 | C．5 | D．6 |
型血有400人，A型血有300人，B型血有200人，AB型血有100人，为了研究血型与性格的关系，按照分层抽样的方法从中抽取样本. 如果从A型血中抽取了12人，则从AB型血中应当抽取的人数为（ ）
下列说法中正确的有（ ）
| A．一组数据的平均数一定大于这组数据中的每个数据 |
| B．一组数据不可能有两个众数 |
| C．一组数据的中位数一定是这组数据中的某个数据 |
| D．一组数据的方差越大，说明这组数据的波动越大 |