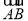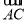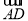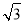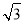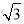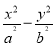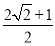题目内容
设Sn为数列{an}的前n项和，Sn＝(－1)nan－
，n∈N*，则：
(1)a3＝________；
(2)S1＋S2＋…＋S100＝________.
(1)－
(2)
【解析】(1)∵Sn＝(－1)nan－
.
当n＝3时，a1＋a2＋a3＝－a3－
，①
当n＝4时，a1＋a2＋a3＋a4＝a4－
，
∴a1＋a2＋a3＝－
，②由①②知a3＝－，
(2)n>1时，Sn－1＝(－1)n－1an－1－
n－1，∴an＝(－1)nan＋(－1)nan－1＋
n.
当n为奇数时，an＝
n＋1－
an－1；当n为偶数时，an－1＝－
n.
故an＝
∴Sn＝
∴S1＋S2＋…＋S100＝－
＝－
＝－
＝
.
练习册系列答案
期末100分闯关海淀考王系列答案
相关题目
