题目内容
已知等差数列{an}的首项a1=1，公差d＞0，且其第二项、第五项、第十四项分别是{bn}等比数列的第二、三、四项；
（1）求数列{an}与{bn}的通项公式；
（2）设数列{cn}对任意自然数n均有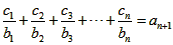
成立，求
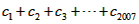的值。
（1）求数列{an}与{bn}的通项公式；
（2）设数列{cn}对任意自然数n均有
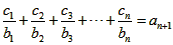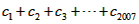成立，求的值。解：(1)由题意得(a1+d)(a1+13d)=(a1+4d)2(d＞0)，
解得d=2，∴an=2n-1，可得bn=3n-1；
(2)当n=1时，c1=3；当n≥2时，由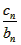
=an+1-an，得cn=2·3n-1，故cn=
，
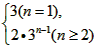故c1+c2+c3+…+c2007=3+2×3+2×32+…+2×32006=32007
解得d=2，∴an=2n-1，可得bn=3n-1；
(2)当n=1时，c1=3；当n≥2时，由
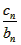=an+1-an，得cn=2·3n-1，故cn=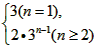， 故c1+c2+c3+…+c2007=3+2×3+2×32+…+2×32006=32007
练习册系列答案
相关题目
已知等差数列{an}中，a4a6=-4，a2+a8=0，n∈N*．