题目内容
设函数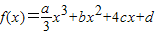 的图象关于原点对称,且f(x)的图象在点p(1,m)处的切线的斜率为-6,且当x=2时,f(x)有极值.
的图象关于原点对称,且f(x)的图象在点p(1,m)处的切线的斜率为-6,且当x=2时,f(x)有极值.(1)求a,b,c,d的值;
(2)若x1,x2∈[-1,1]时,求证
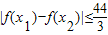 .
.
【答案】分析:(1)由函数f(x)的图象关于原点对称,得f(-x)=-f(x)从而可求b=0,d=0;利用在x=1处的切线方程,只须求出其斜率的值即可,故先利用导数求出在x=1处的导函数值,再结合导数的几何意义即可求出切线的斜率.从而问题解决.
(2)把(1)求出的实数a、b、c、d的值代入函数中确定出解析式,当x∈[-1,1]时,f′(x)<0,从而f(x)在[-1,1]上为减函数,进而可得结论.
解答:解:(1)由函数f(x)的图象关于原点对称,得f(-x)=-f(x)
∴ ,∴b=0,d=0.
,∴b=0,d=0.
∴ ,∴f'(x)=ax2+4c.
,∴f'(x)=ax2+4c.
∴ ,即
,即  .∴a=2,c=-2.
.∴a=2,c=-2.
(2) ,当x∈[-1,1]时,f′(x)<0,
,当x∈[-1,1]时,f′(x)<0,
∴f(x)在[-1,1]上为减函数,若x1,x2∈[-1,1]时,
 .
.
点评:本题以函数的性质为载体,考查函数的解析式,考查利用导数确定函数的单调性,解题的关键是利用单调性确定函数的最值.
(2)把(1)求出的实数a、b、c、d的值代入函数中确定出解析式,当x∈[-1,1]时,f′(x)<0,从而f(x)在[-1,1]上为减函数,进而可得结论.
解答:解:(1)由函数f(x)的图象关于原点对称,得f(-x)=-f(x)
∴
 ,∴b=0,d=0.
,∴b=0,d=0.∴
 ,∴f'(x)=ax2+4c.
,∴f'(x)=ax2+4c.∴
 ,即
,即  .∴a=2,c=-2.
.∴a=2,c=-2.(2)
 ,当x∈[-1,1]时,f′(x)<0,
,当x∈[-1,1]时,f′(x)<0,∴f(x)在[-1,1]上为减函数,若x1,x2∈[-1,1]时,
 .
.点评:本题以函数的性质为载体,考查函数的解析式,考查利用导数确定函数的单调性,解题的关键是利用单调性确定函数的最值.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
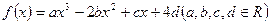 的图象关于原点对称,且
的图象关于原点对称,且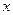 =1时,f(x)取极小值
=1时,f(x)取极小值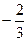 。
。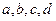 的值;
的值; 时,求证:
时,求证: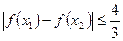 。
。 的图象关于原点对称,f(x)的图象在点P(1,m)处的切线的斜率为-6,且当x=2时f(x)有极值.
的图象关于原点对称,f(x)的图象在点P(1,m)处的切线的斜率为-6,且当x=2时f(x)有极值.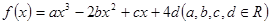 的图象关于原点对称,且
的图象关于原点对称,且 =1时,f(x)取极小值
=1时,f(x)取极小值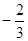 。
。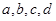 的值;
的值;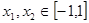 时,求证:
时,求证: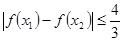 。
。