题目内容
整数集合内不等式(
)4-x2<(
)2a-2x的解集是{1},求实数a的范围.
| 1 |
| 2 |
| 1 |
| 2 |
由题意(
)4-x2<(
)2a-2x,由于y=(
)x是一个减函数
∴4-x2>2a-2x,即x2-2x+2a-4<0,令f(x)=x2-2x+2a-4
由于整数集合内不等式(
)4-x2<(
)2a-2x的解集是{1},
所以有
,解得2≤a<2.5
答:实数a的范围是4≤a<5
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴4-x2>2a-2x,即x2-2x+2a-4<0,令f(x)=x2-2x+2a-4
由于整数集合内不等式(
| 1 |
| 2 |
| 1 |
| 2 |
所以有
|
答:实数a的范围是4≤a<5

练习册系列答案
 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案 小学能力测试卷系列答案
小学能力测试卷系列答案
相关题目
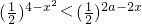 的解集是{1},求实数a的范围.
的解集是{1},求实数a的范围.