题目内容
已知函数 ,
, .
.
(1)求 的极值点;
的极值点;
(2)对任意的 ,记
,记 在
在 上的最小值为
上的最小值为 ,求
,求 的最小值.
的最小值.
【答案】
(1)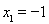 是极大值点,
是极大值点,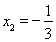 是极小值点;(2)
是极小值点;(2)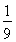 .
.
【解析】
试题分析:(1)利用导数求出函数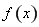 的两个极值点,并结合导数符号确定相应的极大值点与极小值点;(2)在(1)的基础上,对
的两个极值点,并结合导数符号确定相应的极大值点与极小值点;(2)在(1)的基础上,对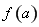 与极小值
与极小值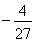 的大小作分类讨论,结合图象确定
的大小作分类讨论,结合图象确定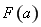 的表达式,然后再根据
的表达式,然后再根据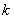 的表达式确定相应的最小值.
的表达式确定相应的最小值.
试题解析:(1)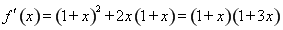 ,
,
由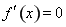 解得:
解得: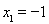 ,
,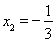 ,
,
当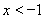 或
或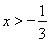 时,
时,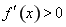 ,
,
当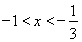 时,
时,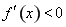
所以,有两个极值点:
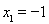 是极大值点,
是极大值点,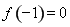 ;
;
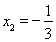 是极小值点,
是极小值点,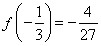 ;
;
(2)过点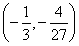 作直线
作直线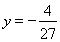 ,与
,与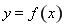 的图象的另一个交点为
的图象的另一个交点为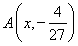 ,
,
则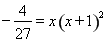 ,即
,即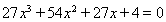 ,
,
已知有解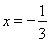 ,则
,则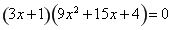 ,
,
解得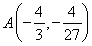 ,
,
当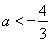 时,
时,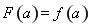 ;
;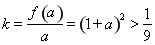 ;
;
当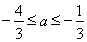 时,
时,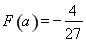 ,
, ,
,
其中当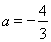 时,
时,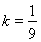 ;
;
当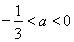 时,
时,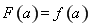 ,
,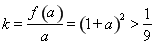 ;
;
所以,对任意的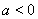 ,
,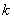 的最小值为
的最小值为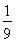 (其中当
(其中当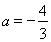 时,
时,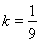 ).
).
考点:1.利用导数求函数的极值;2.分类讨论.

练习册系列答案
相关题目