题目内容
下列结论正确的是( )A.函数
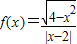 是偶函数
是偶函数B.函数y=x2-4x-3在(2,+∞)上是减函数
C.函数
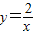 在R上是减函数
在R上是减函数D.函数f(x)=|x+1|-|x-1|是奇函数
【答案】分析:可根据奇偶函数的定义直接判断A与D,根据二次函数的性质与双曲函数y=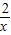 的性质判断B与C.
的性质判断B与C.
解答:解:对于A,f(-x)=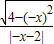 ≠f(x),排除A;
≠f(x),排除A;
对于D,,f(-x)=|-x+1|-|-x-1|=-(|x+1|-|x-1|)=-f(x),f(x)=|x+1|-|x-1|是奇函数,故D正确;
对于B,y=x2-4x-3的开口向上,对称轴为x=2,在(2,+∞)上是增函数,故B错误;
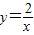 在(-∞,0),(0,+∞)上是减函数,故C错误.
在(-∞,0),(0,+∞)上是减函数,故C错误.
故选D.
点评:本题考查函数奇偶性与单调性的判断,关键在于掌握函数奇偶性与单调性的定义及常见的初等函数的性质,属于中档题.
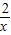 的性质判断B与C.
的性质判断B与C.解答:解:对于A,f(-x)=
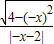 ≠f(x),排除A;
≠f(x),排除A;对于D,,f(-x)=|-x+1|-|-x-1|=-(|x+1|-|x-1|)=-f(x),f(x)=|x+1|-|x-1|是奇函数,故D正确;
对于B,y=x2-4x-3的开口向上,对称轴为x=2,在(2,+∞)上是增函数,故B错误;
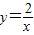 在(-∞,0),(0,+∞)上是减函数,故C错误.
在(-∞,0),(0,+∞)上是减函数,故C错误.故选D.
点评:本题考查函数奇偶性与单调性的判断,关键在于掌握函数奇偶性与单调性的定义及常见的初等函数的性质,属于中档题.

练习册系列答案
 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案
相关题目
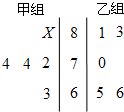 如图所示茎叶图记录了甲乙两组各5名同学的数学成绩.甲组成绩中有一个数据模糊,无法确认,在图中以X表示.若两个小组的平均成绩相同,则下列结论正确的是( )
如图所示茎叶图记录了甲乙两组各5名同学的数学成绩.甲组成绩中有一个数据模糊,无法确认,在图中以X表示.若两个小组的平均成绩相同,则下列结论正确的是( )| A、X=2,S甲2<S乙2 | B、X=2,S甲2>S乙2 | C、X=6,S甲2<S乙2 | D、X=6,2,S甲2>S乙2 |