题目内容
已知函数f(x)=ex-ln(x+1)。(e是自然对数的底数)
(1)判断f(x)在[0,+∞)上是否是单调函数,并写出f(x)在该区间上的最小值;
(2)证明: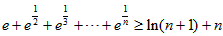 (n∈N*)。
(n∈N*)。
(1)判断f(x)
(2)证明:
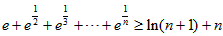 (n∈N*)。
(n∈N*)。 解:(1)∵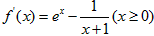 ,
,
令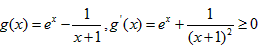 ,
,
∴g(x)在[0,+∞)单增,g(x)≥g(0)=0,
∴f(x)在[0,+∞)单增,所以最小值为f(0)=1;
(2)由(1)知当x=0时,f(x)取得最小值,即f(x)≥f(0)=1,
∴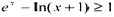 ,即
,即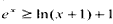 ,
,
取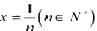 ,则
,则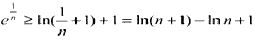 ,
,
于是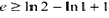
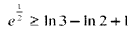
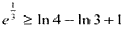
…
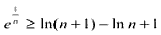
相加得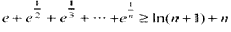 ,故得证。
,故得证。
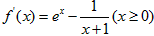 ,
,令
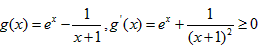 ,
,∴g(x)在[0,+∞)单增,g(x)≥g(0)=0,
∴f(x)在[0,+∞)单增,所以最小值为f(0)=1;
(2)由(1)知当x=0时,f(x)取得最小值,即f(x)≥f(0)=1,
∴
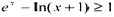 ,即
,即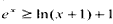 ,
,取
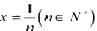 ,则
,则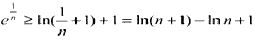 ,
,于是
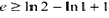
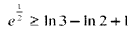
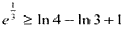
…
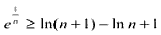
相加得
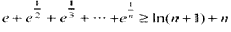 ,故得证。
,故得证。
练习册系列答案
相关题目