题目内容
设x,y为正数,且(x-1)(y-1)=4,则
- A.0<x+y≤6
- B.x+y≥6
- C.

- D.

B
分析:设x+y=t,利用基本不等式可得关于t的不等式,由此可求出x+y的范围
解答:∵(x-1)(y-1)=4,
∴xy-(x+y)=3
设x+y=t,(t>0)
∵x,y都是正数
∴xy≤ =
=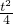 (当且仅当x=y时,取等号)
(当且仅当x=y时,取等号)
∵xy-(x+y)=3
∴xy=3+(x+y)
∴3+t
∴t2-4t-12≥0
∵t>0
∴t≥6
即x+y≥6
故选B
点评:本题考查的重点是基本不等式的运用,考查解一元二次不等式,解题的关键是构建不等式,属于基础题
分析:设x+y=t,利用基本不等式可得关于t的不等式,由此可求出x+y的范围
解答:∵(x-1)(y-1)=4,
∴xy-(x+y)=3
设x+y=t,(t>0)
∵x,y都是正数
∴xy≤
 =
=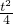 (当且仅当x=y时,取等号)
(当且仅当x=y时,取等号)∵xy-(x+y)=3
∴xy=3+(x+y)
∴3+t

∴t2-4t-12≥0
∵t>0
∴t≥6
即x+y≥6
故选B
点评:本题考查的重点是基本不等式的运用,考查解一元二次不等式,解题的关键是构建不等式,属于基础题

练习册系列答案
相关题目
 则( )
则( ) B.
B.
 D.
D.