题目内容
 如图,已知
如图,已知 ABC中的两条角平分线
ABC中的两条角平分线 和
和 相交于
相交于 ,
, B=60
B=60 ,
, 在
在 上,且
上,且 。
。
(1)证明: 四点共圆;
四点共圆;
(2)证明:CE平分 DEF。
DEF。
【答案】
解析:
 (Ⅰ)在△ABC中,因为∠B=60°,
(Ⅰ)在△ABC中,因为∠B=60°,
所以∠BAC+∠BCA=120°.
因为AD,CE是角平分线,
所以∠HAC+∠HCA=60°,
故∠AHC=120°.
于是∠EHD=∠AHC=120°.
因为∠EBD+∠EHD=180°,
所以B,D,H,E四点共圆。
(Ⅱ)连结BH,则BH为 的平分线,得
的平分线,得 30°
30°
由(Ⅰ)知B,D,H,E四点共圆,
所以 30°
30°
又 60°,由已知可得
60°,由已知可得 ,
,
可得 30°
30°
所以CE平分

练习册系列答案
相关题目
 如图,已知△ABC中的两条角平分线AD和CE相交于H,∠B=60°,F在AC上,
如图,已知△ABC中的两条角平分线AD和CE相交于H,∠B=60°,F在AC上, 如图,已知
如图,已知
 ABC中的两条角平分线
ABC中的两条角平分线 和
和 相交于
相交于 ,
, B=60
B=60 ,
, 在
在 上,且
上,且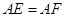 。
。  四点共圆;
四点共圆;