题目内容
定义在[-1,1]上的奇函数f(x),已知当x∈[-1,0]时,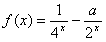 (a∈R),
(a∈R),
(Ⅰ)写出f(x)在[0,1]上的解析式;
(Ⅱ)求f(x)在[0,1]上的最大值;
(Ⅲ)若f(x)是[0,1]上的增函数,求实数a的取值范围。
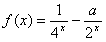 (a∈R),
(a∈R),(Ⅰ)写出f(x)在[0,1]上的解析式;
(Ⅱ)求f(x)在[0,1]上的最大值;
(Ⅲ)若f(x)是[0,1]上的增函数,求实数a的取值范围。
解:(Ⅰ)设x∈[0,1],则-x∈[-1,0],
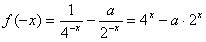 ,
,
∴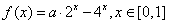 ;
;
(Ⅱ)∵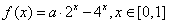 ,
,
令t=2x,t∈[1,2],
∴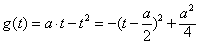 ,
,
当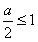 ,即a≤2时,g(t)max=g(1)=a-1;
,即a≤2时,g(t)max=g(1)=a-1;
当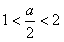 ,即2<a<4时,
,即2<a<4时,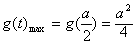 ;
;
当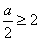 ,即a≥4时,g(t)max=g(2)=2a-4;
,即a≥4时,g(t)max=g(2)=2a-4;
综上:当a≤2时,f(x)最大的值为a-1;当2<a<4时,f(x)最大值为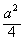 ;当a≥4时,f(x)最大值为2a-4。
;当a≥4时,f(x)最大值为2a-4。
(Ⅲ)因为函数f(x)在[0,1]上是增函数,
所以f′(x)=aln2·2x-ln4·4x=2xln2(a-2·2x)≥0恒成立,
∴a-2·2x≥0恒成立,a≥2·2x恒成立,
∵2x∈[ 1,2],
∴a≥4.
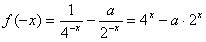 ,
,∴
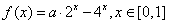 ;
; (Ⅱ)∵
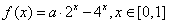 ,
,令t=2x,t∈[1,2],
∴
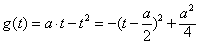 ,
,当
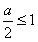 ,即a≤2时,g(t)max=g(1)=a-1;
,即a≤2时,g(t)max=g(1)=a-1;当
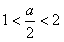 ,即2<a<4时,
,即2<a<4时,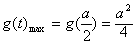 ;
;当
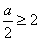 ,即a≥4时,g(t)max=g(2)=2a-4;
,即a≥4时,g(t)max=g(2)=2a-4;综上:当a≤2时,f(x)最大的值为a-1;当2<a<4时,f(x)最大值为
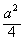 ;当a≥4时,f(x)最大值为2a-4。
;当a≥4时,f(x)最大值为2a-4。 (Ⅲ)因为函数f(x)在[0,1]上是增函数,
所以f′(x)=aln2·2x-ln4·4x=2xln2(a-2·2x)≥0恒成立,
∴a-2·2x≥0恒成立,a≥2·2x恒成立,
∵2x∈[ 1,2],
∴a≥4.

练习册系列答案
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案 走进文言文系列答案
走进文言文系列答案
相关题目