题目内容
【题目】如图，在三棱锥
中， 
， 
， 
，平面
平面
， 
、
分别为
、
中点．
（1）求证： 
；
（2）求二面角
的大小．
【答案】(1)证明见解析；(2)60°.
【解析】试题分析：
（1）连结PD，由题意可得
,则AB⊥平面PDE， 
；
（2）法一：结合几何关系做出二面角的平面角，计算可得其正切值为
，故二面角的
大小为
；
法二：以D为原点建立空间直角坐标系，计算可得平面PBE的法向量
．平面PAB的法向量为
．据此计算可得二面角的
大小为
.
试题解析：
（1）连结PD，
PA=PB，
PD
AB． 
，BCAB，DEAB．
又
，AB平面PDE，PE平面PDE，
∴ABPE．
（2）法一：
平面PAB平面ABC
平面ABC=AB，PDAB，PD平面ABC．
则DEPD,又EDAB，PD平面AB=D，DE平面PAB,
过D做DF垂直PB与F，连接EF，则EFPB，∠DFE为所求二面角的平面角，
则：DE=
，DF=
，则
，故二面角的
大小为
法二：
平面PAB平面ABC，平面PAB平面ABC=AB，PDAB，PD平面ABC．
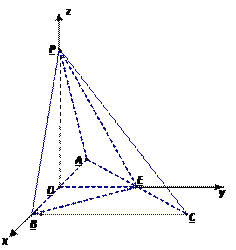
如图，以D为原点建立空间直角坐标系，
B(1，0，0)，P(0，0，
)，E(0， 
，0)，
=(1，0， 
)， 
=(0， 
， 
）．
设平面PBE的法向量
，
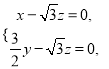令
，得
．
DE
平面PAB， 
平面PAB的法向量为
．
设二面角的
大小为
，由图知，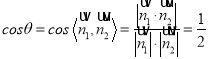 
，
所以
即二面角的
大小为
.
【题目】2016年1月1日起全国统一实施全面两孩政策．为了解适龄民众对放开生育二胎政策的态度，某市选取70后和80后作为调查对象，随机调查了100位，得到数据如表：
生二胎 | 不生二胎 | 合计 | |
70后 | 30 | 15 | 45 |
80后 | 45 | 10 | 55 |
合计 | 75 | 25 | 100 |
（1）以这100个人的样本数据估计该市的总体数据，且以频率估计概率，若从该市70后公民中随机抽取3位，记其中生二胎的人数为X，求随机变量X的分布列和数学期望；
（2）根据调查数据，是否有90%以上的把握认为“生二胎与年龄有关”，并说明理由．
参考数据：
P（K2＞k） | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 |
k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 |
（参考公式： 
，其中n=a+b+c+d）
