题目内容
对于给定的实数a、b,定义运算“⊕”: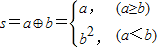 .则集合{y|y=(1⊕x)•x+(2⊕x),x∈[-2,2]}的最大元素是 .
.则集合{y|y=(1⊕x)•x+(2⊕x),x∈[-2,2]}的最大元素是 .
【答案】分析:先根据新定义求出1⊕x和2⊕x的数值,然后分类讨论求出y的取值范围.
解答:解:根据新定义可知1⊕x= ,2⊕x=
,2⊕x= ,
,
因为x∈[-2,2],所以2⊕x=2.
若-2≤x≤1时,1⊕x=1,2⊕x=2,所以y=(1⊕x)•x+(2⊕x)=x+2,此时0≤x+2≤3.即0≤y≤3.
若1<x≤2时,1⊕x=x2,2⊕x=2,所以y=(1⊕x)•x+(2⊕x)=x3+2,此时3<y≤10.
综上0≤y≤10,即集合{y|0≤y≤10}.
所以集合元素的最大元素为10.
故答案为:10.
点评:本题的考点是新定义的应用,以及求分段函数的值域问题.
解答:解:根据新定义可知1⊕x=
 ,2⊕x=
,2⊕x= ,
,因为x∈[-2,2],所以2⊕x=2.
若-2≤x≤1时,1⊕x=1,2⊕x=2,所以y=(1⊕x)•x+(2⊕x)=x+2,此时0≤x+2≤3.即0≤y≤3.
若1<x≤2时,1⊕x=x2,2⊕x=2,所以y=(1⊕x)•x+(2⊕x)=x3+2,此时3<y≤10.
综上0≤y≤10,即集合{y|0≤y≤10}.
所以集合元素的最大元素为10.
故答案为:10.
点评:本题的考点是新定义的应用,以及求分段函数的值域问题.

练习册系列答案
 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案
相关题目
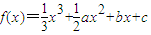 ,其中a,b,c∈R.
,其中a,b,c∈R.