题目内容
求证:在直角三角形中,三条边的长成等差数列的充要条件是它们的比为3∶4∶5.
答案:
解析:
解析:
证明:(1)必要性 假定直角三角形三条边的长成等差数列,将这三条边的长从小到大排列,它们可以表示为a-d,a,a+d,这里a-d>0,d>0. 由于它们是直角三角形的三条边的长. ∴(a-d)2+a2=(a+d)2,即a=4d. 从而这三条边的长是3d,4d,5d. 因此,这三条边的长的比是3∶4∶5. (2)充分性 如果直角三角形三条边的长a,b,c的比为3∶4∶5,那么可设,a=3k,b=4k,c=5k,(k>0) ∵b-a=k,c-b=k,∴b-a=c-b 即a,b,c成等差数列. 综上,命题得证. |

练习册系列答案
相关题目
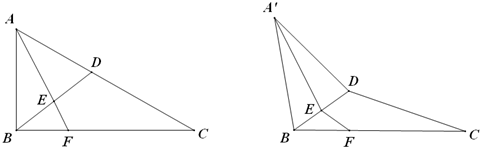
 中,
中, 是
是 边上的高,
边上的高, ,
, ,
, 分别为垂足,求证:
分别为垂足,求证: .
.
