题目内容
函数y=x2-2x+3在定义域[m，3]上的值域为[2，6]，则m的取值范围是
- A.（0，3]
- B.[0，3）
- C.[-1，1]
- D.[0，1]
C
分析：由已知函数的解析式，我们可以判断出函数图象的形状及最值，根据函数y=x2-2x+3在定义域[m，3]上的值域为[2，6]，易结合二次函数的图象和性质得到答案．
解答：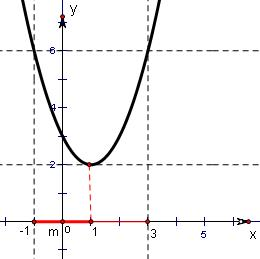
解：∵函数y=x2-2x+3的图象是开口方向朝上，以直线x=1为对称轴的抛物线；
且f（-1）=f（3）=6，f（1）=2，如图．
若定义域为[m，3]，值域为[2，6]，
则-1≤m≤1．
故选C．
点评：本题考查的知识点是二次函数的性质，其中根据已知条件确定二次函数的图象和性质，是解答本题的关键．
分析：由已知函数的解析式，我们可以判断出函数图象的形状及最值，根据函数y=x2-2x+3在定义域[m，3]上的值域为[2，6]，易结合二次函数的图象和性质得到答案．
解答：
解：∵函数y=x2-2x+3的图象是开口方向朝上，以直线x=1为对称轴的抛物线；且f（-1）=f（3）=6，f（1）=2，如图．
若定义域为[m，3]，值域为[2，6]，
则-1≤m≤1．
故选C．
点评：本题考查的知识点是二次函数的性质，其中根据已知条件确定二次函数的图象和性质，是解答本题的关键．
练习册系列答案
相关题目