Question

【题目】已知圆与轴交于两点，点为圆上异于的任意一点，圆在点处的切线与圆在点处的切线分别交于，直线和交于点，设点的轨迹为曲线.

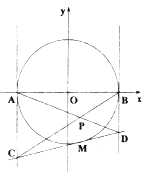
（1）求曲线的方程；

（2）曲线与轴正半轴交点为，则曲线是否存在直角顶点为的内接等腰直角三角形，若存在，求出所有满足条件的的两条直角边所在直线的方程，若不存在，请说明理由.

Answer 1

【答案】（1）（2）详见解

【解析】试题分析：（1）设，则处的切线为，切线CD与AC,BD组方程组可求得C,D点坐标，再直线AD,BC组方程组，解点交点P轨迹方程。注意消参，需要用到点M在圆上。同时注意曲线方程变量范围。（2）设，则， 与椭圆组方程组，可求得GH,同理求得，再利用进行分类讨论。

试题解析：（Ⅰ）设，则处的切线为，

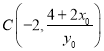则， ，则，则；

（Ⅱ）由于直线不与坐标轴平行或垂直，可设，则

，得，由于恒成立，设两个根为，

则，同理，

由知： ，得：

（1）时，得得： 或

（2）时，得得： 或

综上，共分三种情况

（1）两条直角边所在直线方程为： ；

（2）两条直角边所在直线方程为：

（3）两条直角边所在直线方程为：